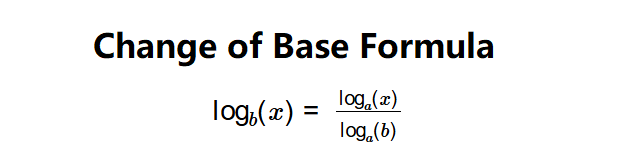Change of Base Calculator

1. What is a Change of Base Calculator?

Definition: This calculator computes the logarithm of a number \( x \) with respect to a new base \( b \), given the argument \( x \), original base \( a \), and new base \( b \). It uses the change of base formula to convert \( \log_a(x) \) to \( \log_b(x) \).

Purpose: It aids in mathematics, science, and engineering by allowing users to express logarithms in different bases, useful in calculations where a specific base is required (e.g., base 10 for decibels, base 2 for computing).

2. How Does the Calculator Work?

The calculator uses the following formula:

Change of Base: \( \log_b(x) = \frac{\log_a(x)}{\log_a(b)} \)

Steps:

Input the argument \( x \) (positive), original base \( a \) (positive, not 1), and new base \( b \) (positive, not 1).
Validate inputs (\( x > 0 \), \( a > 0 \), \( a \neq 1 \), \( b > 0 \), \( b \neq 1 \)).
Compute the logarithm using the change of base formula, implemented as \( \log_b(x) = \frac{\ln(x)}{\ln(b)} \) for accuracy.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of Change of Base Calculations

Calculating logarithms with different bases is essential for:

Mathematics Education: Understanding the properties of logarithms and their flexibility across bases.
Science and Engineering: Converting logarithmic scales (e.g., from base 10 to base e in calculus or base 2 in information theory).
Computing: Working with logarithms in algorithms or data structures that require specific bases.

4. Using the Calculator

Examples:

Example 1: Argument \( x = 100 \), Original base \( a = 10 \), New base \( b = 2 \)
Result: \( \log_2(100) = \frac{\log_{10}(100)}{\log_{10}(2)} \approx \frac{2}{0.3010} \approx 6.6439 \).
Example 2: Argument \( x = 8 \), Original base \( a = 2 \), New base \( b = 10 \)
Result: \( \log_{10}(8) = \frac{\log_2(8)}{\log_2(10)} \approx \frac{3}{3.3219} \approx 0.9031 \).
Example 3: Argument \( x = 2.7183 \), Original base \( a = 10 \), New base \( b = e \)
Result: \( \log_e(2.7183) \approx \frac{\ln(2.7183)}{\ln(e)} \approx \frac{1}{1} = 1.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What is the change of base formula?
A: The change of base formula allows a logarithm in one base to be expressed in another base: \( \log_b(x) = \frac{\log_a(x)}{\log_a(b)} \).

Q: Why can’t the base be 1?
A: The logarithm with base 1 is undefined because \( 1^y = 1 \) for all \( y \), so it cannot produce a unique value.

Q: Why must the argument be positive?
A: Logarithms are defined only for positive arguments in the real number system, as there is no real number \( y \) such that \( b^y \leq 0 \).