1. What is a Centroid of a Triangle Calculator?

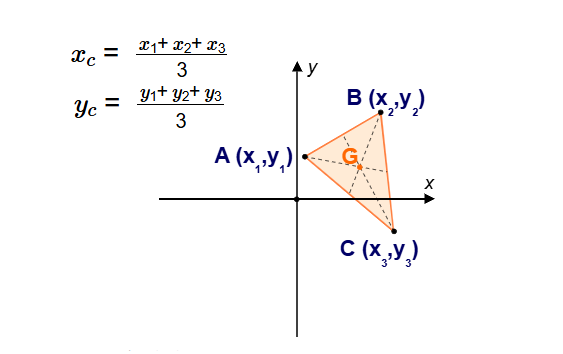
Definition: This calculator determines the centroid of a triangle given the coordinates of its three vertices \( (x_1, y_1) \), \( (x_2, y_2) \), and \( (x_3, y_3) \). The centroid is the point where the triangle's medians intersect, and it divides each median in a 2:1 ratio. All inputs and outputs are treated as unitless numbers.

Purpose: It aids in geometry education and practical applications by finding the centroid, useful in fields like engineering, computer graphics, and physics for determining the center of mass of triangular shapes.

2. How Does the Calculator Work?

The calculator uses the following formulas to find the centroid \( (x_c, y_c) \):

• \( x_c = \frac{x_1 + x_2 + x_3}{3} \)
• \( y_c = \frac{y_1 + y_2 + y_3}{3} \)

Steps:

• Input the coordinates of the three vertices as unitless numbers.
• Validate inputs: ensure the points are not collinear by checking the triangle's area.
• Compute the centroid coordinates by averaging the \( x \)- and \( y \)-coordinates of the vertices.
• Display the results to 4 decimal places.

3. Importance of Centroid of a Triangle Calculations

Centroid calculations are essential for:

• Geometry: Understanding the properties of triangles and their medians.
• Physics: Determining the center of mass of a triangular object, assuming uniform density.
• Computer Graphics: Positioning triangular elements in 2D graphics or simulations.

4. Using the Calculator

Examples:

• Example 1: Vertices \( (0, 0) \), \( (3, 0) \), \( (0, 4) \), Centroid
  Centroid: \( (x_c, y_c) = \left( \frac{0 + 3 + 0}{3}, \frac{0 + 0 + 4}{3} \right) = (1, \frac{4}{3}) \) = (1.0000, 1.3333).
• Example 2: Vertices \( (1, 1) \), \( (5, 1) \), \( (3, 4) \), Centroid
  Centroid: \( (x_c, y_c) = \left( \frac{1 + 5 + 3}{3}, \frac{1 + 1 + 4}{3} \right) = (3, 2) \) = (3.0000, 2.0000).
• Example 3: Vertices \( (-2, 3) \), \( (4, 3) \), \( (1, 7) \), Centroid
  Centroid: \( (x_c, y_c) = \left( \frac{-2 + 4 + 1}{3}, \frac{3 + 3 + 7}{3} \right) = (1, \frac{13}{3}) \) = (1.0000, 4.3333).

5. Frequently Asked Questions (FAQ)

Q: What is the centroid of a triangle?
A: The centroid is the point where the three medians of a triangle intersect. It divides each median in a 2:1 ratio and is also the triangle's center of mass if the density is uniform.

Q: Why must the points not be collinear?
A: If the points are collinear (lie on a straight line), they do not form a triangle, and the centroid is undefined. The calculator uses the Shoelace formula to check for collinearity.

Q: Can this calculator be used for any triangle?
A: Yes, the centroid formula applies to any triangle (e.g., right, isosceles, scalene) as long as the vertices form a triangle.

Centroid of a Triangle Calculator© - All Rights Reserved 2025