Central Angle Calculator

Mode:

Arc Length \( L \):

Radius \( r \):

Diameter \( 2r \):

Central Angle \( \theta \) (radians):

rad

Central Angle \( \theta \) (degrees):

deg

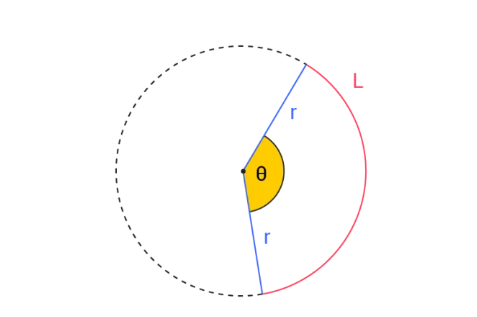
1. What is a Central Angle Calculator?

Definition: This calculator computes the central angle of a circle and its diameter based on the arc length and radius. A central angle is an angle with its vertex at the center of a circle, formed by two radii that extend to the circumference.

Purpose: It is useful in geometry, physics, and engineering to determine angular measurements and circle properties for applications like navigation, astronomy, and design.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Diameter \( 2r \): \( 2r \)
Central Angle \( \theta \) (radians): \( \theta = \frac{L}{r} \)
Central Angle \( \theta \) (degrees): \( \theta_{\text{deg}} = \theta_{\text{rad}} \times \frac{180}{\pi} \)

Unit Conversions:

Input Dimensions: m, cm (1 m = 100 cm), mm (1 m = 1000 mm), in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
Output Dimensions: m, cm, mm, in, ft, yd (for diameter only)

Steps:

Input the arc length \( L \) and radius \( r \) with their respective units.
Convert inputs to meters for calculation.
Validate inputs (must be positive).
Calculate the diameter and central angle using the formulas above.
Convert the diameter to the selected output unit and display the central angle in both radians and degrees.
Format outputs to 4 decimal places or scientific notation for small values.

3. Importance of Central Angle Calculations

Calculating the central angle is crucial for:

Geometry Education: Understanding angular relationships in circles.
Navigation and Astronomy: Determining angular distances, such as the angle between stars or satellites.
Engineering and Design: Designing circular components like gears, wheels, or arches.

4. Using the Calculator

Examples:

Example 1: Arc Length \( L = 5 \, \text{cm} \), Radius \( r = 2 \, \text{cm} \)
- Convert: \( L = 0.05 \, \text{m} \), \( r = 0.02 \, \text{m} \)
- Diameter: \( 2r = 2 \times 0.02 = 0.04 \, \text{m} = 4 \, \text{cm} \)
- Central Angle (radians): \( \theta = \frac{0.05}{0.02} = 2.5 \, \text{rad} \)
- Central Angle (degrees): \( \theta_{\text{deg}} = 2.5 \times \frac{180}{\pi} \approx 143.2394 \, \text{deg} \)
Example 2: Arc Length \( L = 10 \, \text{m} \), Radius \( r = 4 \, \text{m} \)
- Diameter: \( 2r = 2 \times 4 = 8 \, \text{m} \)
- Central Angle (radians): \( \theta = \frac{10}{4} = 2.5 \, \text{rad} \)
- Central Angle (degrees): \( \theta_{\text{deg}} = 2.5 \times \frac{180}{\pi} \approx 143.2394 \, \text{deg} \)

5. Frequently Asked Questions (FAQ)

Q: What is a central angle?
A: A central angle is an angle formed by two radii of a circle, with its vertex at the circle's center, subtending an arc on the circumference.

Q: Why is the central angle calculated in both radians and degrees?
A: Radians are unitless and simplify calculations, while degrees are commonly used in practical applications. The calculator provides both for convenience.