Center of Ellipse Calculator

Calculation Method:

\( a \):

\( b \):

\( c_1 \):

\( c_2 \):

1. What is a Center of Ellipse Calculator?

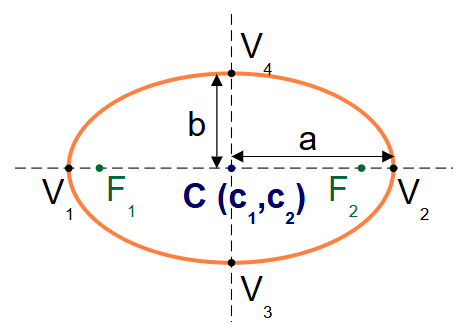
Definition: This calculator determines the center of an ellipse using four methods: the ellipse equation (\( \frac{(x - c_1)^2}{a^2} + \frac{(y - c_2)^2}{b^2} = 1 \)), the vertices (major axis), the co-vertices (minor axis), and the foci. All inputs and outputs are treated as unitless numbers.

Purpose: It aids in geometry education and practical applications by finding the center of an ellipse, useful in fields like engineering, computer graphics, and design where ellipse equations are common.

2. How Does the Calculator Work?

The calculator uses the following methods:

Ellipse Equation: \( \frac{(x - c_1)^2}{a^2} + \frac{(y - c_2)^2}{b^2} = 1 \)

Center: \( (x, y) = (c_1, c_2) \)

Vertices (Major Axis): Using vertices \( V_1 (x_1, y_1) \) and \( V_2 (x_2, y_2) \)

Center: \( (x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \)

Co-Vertices (Minor Axis): Using co-vertices \( V_3 (x_3, y_3) \) and \( V_4 (x_4, y_4) \)

Center: \( (x, y) = \left( \frac{x_3 + x_4}{2}, \frac{y_3 + y_4}{2} \right) \)

Foci: Using foci \( F_1 (x_{f1}, y_{f1}) \) and \( F_2 (x_{f2}, y_{f2}) \)

Center: \( (x, y) = \left( \frac{x_{f1} + x_{f2}}{2}, \frac{y_{f1} + y_{f2}}{2} \right) \)

Steps:

Select the calculation method.
Input the required values as unitless numbers.
Validate inputs: ensure \( a, b > 0 \) (Ellipse Equation), vertices/co-vertices/foci are correctly aligned and distinct.
Compute the center coordinates using the appropriate method.
Display the results to 4 decimal places.

3. Importance of Ellipse Center Calculations

Ellipse center calculations are essential for:

Geometry: Understanding the properties of ellipses in different forms.
Engineering: Designing elliptical components like orbits or structural arches.
Computer Graphics: Positioning ellipses in 2D graphics or animations.

4. Using the Calculator

Examples:

Ellipse Equation: \( a = 5 \), \( b = 3 \), \( c_1 = 2 \), \( c_2 = -1 \), Center
Center: \( (x, y) = (2, -1) \) = (2.0000, -1.0000).
Vertices (Major Axis): \( V_1 (1, 3) \), \( V_2 (5, 3) \), Center
Center: \( (x, y) = \left( \frac{1 + 5}{2}, \frac{3 + 3}{2} \right) = (3, 3) \) = (3.0000, 3.0000).
Co-Vertices (Minor Axis): \( V_3 (-2, 4) \), \( V_4 (-2, 0) \), Center
Center: \( (x, y) = \left( \frac{-2 + (-2)}{2}, \frac{4 + 0}{2} \right) = (-2, 2) \) = (-2.0000, 2.0000).
Foci: \( F_1 (0, 1) \), \( F_2 (4, 1) \), Center
Center: \( (x, y) = \left( \frac{0 + 4}{2}, \frac{1 + 1}{2} \right) = (2, 1) \) = (2.0000, 1.0000).

5. Frequently Asked Questions (FAQ)

Q: What is the center of an ellipse?
A: The center of an ellipse is the point equidistant from its foci and the midpoint of its major and minor axes. It is represented as \( (x, y) \) in the ellipse's equation.

Q: Why must vertices have the same \( y \)-coordinate in the Vertices method?
A: The calculator assumes a horizontal ellipse (major axis along the x-axis), so the vertices must share the same \( y \)-coordinate. For a vertical ellipse, you would use the co-vertices method with the same \( x \)-coordinate.

Q: What happens if the foci are not distinct?
A: If the foci have the same coordinates, they do not define an ellipse (which requires two distinct foci). The calculator will display an error in this case.