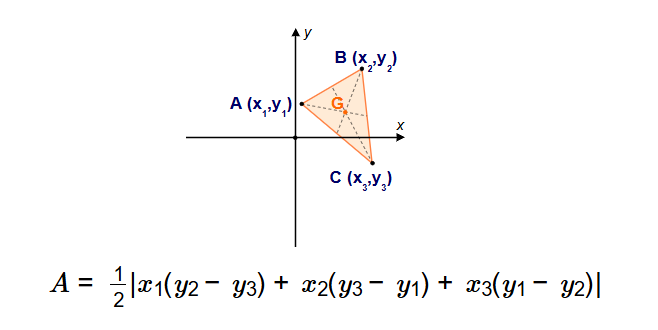Area of a Triangle by Coordinates Calculator

\( x_1 \) (A):

\( y_1 \) (A):

\( x_2 \) (B):

\( y_2 \) (B):

\( x_3 \) (C):

\( y_3 \) (C):

Area:

Perimeter:

1. What is an Area of a Triangle by Coordinates Calculator?

Definition: This calculator computes the area and perimeter of a triangle given the Cartesian coordinates of its three vertices \( A(x_1, y_1) \), \( B(x_2, y_2) \), and \( C(x_3, y_3) \). It uses the Shoelace formula for the area and calculates the perimeter by summing the distances between consecutive vertices. The calculator supports length units (mm, cm, m, in, ft, yd) and area units (mm², cm², m², in², ft², yd²), defaulting to m for inputs and lengths, and m² for area.

Purpose: It aids in geometry education and practical applications by calculating key properties of triangles, useful in fields like surveying, computer graphics, and design where vertex coordinates are known.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Area (Shoelace Formula):

\( A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \)

Perimeter:

Side lengths: \( AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \), \( BC = \sqrt{(x_3 - x_2)^2 + (y_3 - y_2)^2} \), \( CA = \sqrt{(x_1 - x_3)^2 + (y_1 - y_3)^2} \)
Perimeter: \( P = AB + BC + CA \)

Steps:

Input the coordinates of the three vertices, with units defaulting to m.
Select the desired output units for area and perimeter (defaulting to m² and m).
Validate inputs: ensure the points form a triangle (not collinear).
Convert all coordinates to meters for calculation.
Compute the area using the Shoelace formula and the perimeter by summing side lengths.
Convert the results to the selected units.
Display results with lengths and area to 4 decimal places.

3. Importance of Triangle Area by Coordinates Calculations

Triangle area calculations using coordinates are essential for:

Surveying: Determining the area of triangular land plots when vertex coordinates are measured, often in units like meters or feet.
Computer Graphics: Calculating areas of triangular elements in 2D rendering or mesh generation.
Geometry Education: Teaching the Shoelace formula and its application in coordinate geometry.

4. Using the Calculator

Examples:

Example 1: \( A(0, 0) \) m, \( B(3, 0) \) m, \( C(0, 4) \) m, Area in m², Perimeter in m
Area: \( A = \frac{1}{2} \left| 0(0-4) + 3(4-0) + 0(0-0) \right| = \frac{1}{2} \cdot 12 = 6.0000 \) m²
Perimeter: \( AB = 3 \), \( BC = \sqrt{(0-3)^2 + (4-0)^2} = 5 \), \( CA = \sqrt{(0-0)^2 + (0-4)^2} = 4 \), \( P = 3 + 5 + 4 = 12.0000 \) m.
Example 2: \( A(0, 0) \) cm, \( B(50, 0) \) cm, \( C(0, 60) \) cm, Area in cm², Perimeter in cm
Convert to meters: \( A(0, 0) \), \( B(0.5, 0) \), \( C(0, 0.6) \)
Area: \( A = \frac{1}{2} \left| 0(0-0.6) + 0.5(0.6-0) + 0(0-0) \right| = \frac{1}{2} \cdot 0.3 = 0.1500 \) m² = 1500.0000 cm²
Perimeter: \( AB = 0.5 \), \( BC = \sqrt{(0-0.5)^2 + (0.6-0)^2} \approx 0.7810 \), \( CA = 0.6 \), \( P = 0.5 + 0.7810 + 0.6 = 1.8810 \) m = 188.1000 cm.
Example 3: \( A(1, 1) \) ft, \( B(4, 1) \) ft, \( C(1, 5) \) ft, Area in ft², Perimeter in ft
Convert to meters: \( A(0.3048, 0.3048) \), \( B(1.2192, 0.3048) \), \( C(0.3048, 1.5240) \)
Area: \( A = \frac{1}{2} \left| 0.3048(0.3048-1.5240) + 1.2192(1.5240-0.3048) + 0.3048(0.3048-0.3048) \right| \approx 0.5574 \) m² = 6.0000 ft²
Perimeter: \( AB = 0.9144 \), \( BC = \sqrt{(0.3048-1.2192)^2 + (1.5240-0.3048)^2} \approx 1.4142 \), \( CA = 1.2192 \), \( P \approx 3.5478 \) m = 11.6400 ft.

5. Frequently Asked Questions (FAQ)

Q: What is the Shoelace formula?
A: The Shoelace formula (or surveyor's formula) calculates the area of a polygon given its vertices' coordinates. For a triangle, it simplifies to \( A = \frac{1}{2} \left| x_1(y_2 - y_3) + x_2(y_3 - y_1) + x_3(y_1 - y_2) \right| \).

Q: Why do inputs and outputs default to m and m²?
A: Meters (m) and square meters (m²) are the default units to provide a standard metric base, ensuring consistency in calculations, but you can convert to other units as needed.

Q: What does it mean if the area is zero?
A: If the area is zero, the three points are collinear (lie on a straight line) and do not form a triangle. The calculator will display an error in this case.