Angle of Right Triangle Calculator

Hypotenuse \( c \):

Area:

Angle \( \alpha \):

deg

Angle \( \beta \):

deg

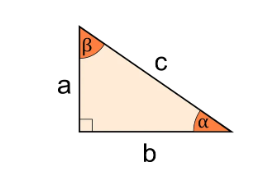
1. What is an Angle of Right Triangle Calculator?

Definition: This calculator computes the hypotenuse, area, and angles of a right triangle given the lengths of its two legs \( a \) and \( b \). It assumes the right angle is at vertex C (\( \gamma = 90^\circ \)), with support for length units (mm, cm, m, in, ft, yd) and area units (mm², cm², m², in², ft², yd²). Outputs default to m for lengths and m² for area, with independent unit conversion for each output.

Purpose: It aids in geometry education and practical applications by determining all properties of a right triangle, useful in fields like engineering, architecture, and physics where right triangles are common.

2. How Does the Calculator Work?

The calculator uses the following formulas for a right triangle:

Hypotenuse: \( c = \sqrt{a^2 + b^2} \)
Area: \( \text{Area} = \frac{1}{2} \cdot a \cdot b \)
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{a}{b}\right) \)
Angle \( \beta \): \( \beta = 90^\circ - \alpha \)

Steps:

Input the lengths of legs \( a \) and \( b \), and select their units (mm, cm, m, in, ft, yd).
Select the desired output units for the hypotenuse and area (defaults to m and m²).
Validate inputs: ensure \( a \) and \( b \) are positive.
Convert all lengths to meters for calculation.
Compute the hypotenuse, area, and angles using the formulas above.
Convert the hypotenuse and area to their selected units, display angles in degrees.
Display results with lengths and area to 4 decimal places, angles to 2 decimal places.

3. Importance of Angle of Right Triangle Calculations

Right triangle calculations are essential for:

Geometry: Solving right triangles, fundamental in trigonometry and geometric applications.
Engineering: Designing structures with right-angled components, with measurements in units like m or ft.
Navigation: Calculating distances and angles, often requiring unit conversions (e.g., m to cm).

4. Using the Calculator

Examples:

Example 1: Legs \( a = 3 \) m, \( b = 4 \) m, Hypotenuse in m, Area in m²
Hypotenuse: \( c = \sqrt{3^2 + 4^2} = 5.0000 \) m
Area: \( \text{Area} = \frac{1}{2} \cdot 3 \cdot 4 = 6.0000 \) m²
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{3}{4}\right) \approx 36.87^\circ \)
Angle \( \beta \): \( \beta = 90^\circ - 36.87^\circ = 53.13^\circ \).
Example 2: Legs \( a = 60 \) cm, \( b = 80 \) cm, Hypotenuse in cm, Area in mm²
Convert to meters: \( a = 0.6 \) m, \( b = 0.8 \) m
Hypotenuse: \( c = \sqrt{0.6^2 + 0.8^2} = 1.0000 \) m = 100.0000 cm
Area in m²: \( \text{Area} = \frac{1}{2} \cdot 0.6 \cdot 0.8 = 0.2400 \) m² = 240000.0000 mm²
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{0.6}{0.8}\right) \approx 36.87^\circ \)
Angle \( \beta \): \( \beta = 53.13^\circ \).
Example 3: Legs \( a = 5 \) ft, \( b = 12 \) ft, Hypotenuse in yd, Area in ft²
Convert to meters: \( a = 5 \cdot 0.3048 = 1.5240 \) m, \( b = 12 \cdot 0.3048 = 3.6576 \) m
Hypotenuse: \( c = \sqrt{1.5240^2 + 3.6576^2} \approx 3.9700 \) m = 4.3333 yd
Area in m²: \( \text{Area} = \frac{1}{2} \cdot 1.5240 \cdot 3.6576 \approx 2.7865 \) m² = 30.0000 ft²
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{1.5240}{3.6576}\right) \approx 22.62^\circ \)
Angle \( \beta \): \( \beta = 67.38^\circ \).

5. Frequently Asked Questions (FAQ)

Q: What is a right triangle?
A: A right triangle has one angle equal to 90 degrees. In this calculator, the right angle is at vertex C (\( \gamma = 90^\circ \)), with \( a \) and \( b \) as the legs and \( c \) as the hypotenuse.

Q: Why do outputs default to m and m²?
A: Meters (m) and square meters (m²) are the default units to provide a standard metric base, but you can convert each output independently to other units like cm, ft, or yd².

Q: How does the calculator handle different units for outputs?
A: Each output (hypotenuse and area) has its own unit dropdown, allowing independent conversion. For example, you can display the hypotenuse in m and the area in ft² without affecting each other.