ABC Triangle Calculator

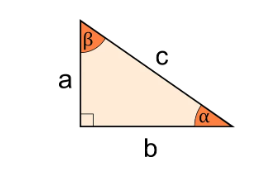
1. What is an ABC Triangle Calculator?

Definition: This calculator solves for the missing dimensions of a right triangle (with right angle \( \gamma = 90^\circ \)) using three different input options: "Two Sides," "Angle and One Side," or "Area and One Side." It calculates sides, angles, and area based on the provided values, assuming the right angle is at vertex C.

Purpose: It aids in geometry education and problem-solving by determining all properties of a right triangle, useful in fields like engineering, physics, and design where right triangles are common.

2. How Does the Calculator Work?

The calculator uses the following methods depending on the selected option:

Two Sides (\( a \), \( b \)):

Hypotenuse: \( c = \sqrt{a^2 + b^2} \)
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{a}{b}\right) \)
Angle \( \beta \): \( \beta = 90^\circ - \alpha \)

Angle and One Side (\( a \), \( \alpha \)):

Angle \( \beta \): \( \beta = 90^\circ - \alpha \)
Side \( b \): \( b = a \cdot \frac{\cos(\alpha)}{\sin(\alpha)} \)
Hypotenuse \( c \): \( c = \frac{a}{\sin(\alpha)} \)
Area: \( \text{Area} = \frac{1}{2} \cdot a \cdot b \)

Area and One Side (\( \text{Area} \), \( a \)):

Side \( b \): \( b = \frac{2 \cdot \text{Area}}{a} \)
Hypotenuse \( c \): \( c = \sqrt{a^2 + b^2} \)
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{a}{b}\right) \)
Angle \( \beta \): \( \beta = 90^\circ - \alpha \)

Steps:

Select the calculation option.
Input the required values.
Validate inputs: ensure sides and area are positive, angles are between 0 and 90 degrees, and angle sums are appropriate.
Apply the relevant formulas to compute the missing values.
Display results with angles to 2 decimal places and lengths/area to 4 decimal places.

3. Importance of ABC Triangle Calculations

ABC triangle calculations are essential for:

Geometry: Solving right triangles, which are fundamental in trigonometry and geometric applications.
Engineering: Designing structures with right-angled components, such as beams and supports.
Physics: Analyzing forces and vectors in two dimensions, often involving right triangles.

4. Using the Calculator

Examples:

Two Sides: Legs \( a = 3 \), \( b = 4 \)
Hypotenuse: \( c = \sqrt{3^2 + 4^2} = \sqrt{25} = 5.0000 \)
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{3}{4}\right) \approx 36.87^\circ \)
Angle \( \beta \): \( \beta = 90^\circ - 36.87^\circ = 53.13^\circ \).
Angle and One Side: Leg \( a = 5 \), \( \alpha = 30^\circ \)
Angle \( \beta \): \( \beta = 90^\circ - 30^\circ = 60.00^\circ \)
Side \( b \): \( b = 5 \cdot \frac{\cos(30^\circ)}{\sin(30^\circ)} = 5 \cdot \sqrt{3} \approx 8.6603 \)
Hypotenuse \( c \): \( c = \frac{5}{\sin(30^\circ)} = 10.0000 \)
Area: \( \text{Area} = \frac{1}{2} \cdot 5 \cdot 8.6603 \approx 21.6508 \).
Area and One Side: Area \( = 6 \), Leg \( a = 3 \)
Side \( b \): \( b = \frac{2 \cdot 6}{3} = 4.0000 \)
Hypotenuse \( c \): \( c = \sqrt{3^2 + 4^2} = 5.0000 \)
Angle \( \alpha \): \( \alpha = \arctan\left(\frac{3}{4}\right) \approx 36.87^\circ \)
Angle \( \beta \): \( \beta = 90^\circ - 36.87^\circ = 53.13^\circ \).

5. Frequently Asked Questions (FAQ)

Q: What does ABC triangle mean?
A: An ABC triangle, in this context, is a right triangle with a right angle at vertex C (\( \gamma = 90^\circ \)). Sides \( a \) and \( b \) are the legs, and \( c \) is the hypotenuse.

Q: Why must angles be less than 90 degrees?
A: Since the triangle is right-angled at \( \gamma \), the other two angles (\( \alpha \) and \( \beta \)) must be less than 90 degrees to ensure the angle sum is 180 degrees.

Q: Can this calculator handle non-right triangles?
A: No, this calculator is designed for right triangles, as specified by the ABC Triangle Calculator on Omni Calculator. For non-right triangles, other methods like the Law of Sines or Cosines would be needed.