1. What is an AAS Triangle Calculator?
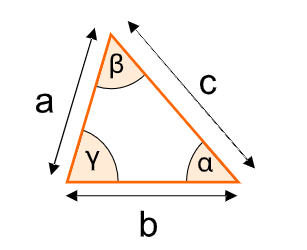
Definition: This calculator computes the missing dimensions of an AAS (Angle-Angle-Side) triangle, where two angles (\( \alpha \), \( \beta \)) and a non-included side (\( a \)) are known. It calculates the third angle (\( \gamma \)), the remaining sides (\( b \), \( c \)), the height (\( h \)), and the area of the triangle.
Purpose: It aids in geometry education and problem-solving by determining all properties of an AAS triangle, useful in fields like trigonometry, engineering, and design where triangles need to be fully defined.
2. How Does the Calculator Work?
The calculator uses the following steps and formulas:
- Third Angle: \( \gamma = 180^\circ - \alpha - \beta \)
- Sides \( b \) and \( c \) (Law of Sines): \( b = a \cdot \frac{\sin(\beta)}{\sin(\alpha)}, \quad c = a \cdot \frac{\sin(\gamma)}{\sin(\alpha)} \)
- Height \( h \) (with \( c \) as base): \( h = a \cdot \sin(\gamma) \)
- Area (using base \( c \) and height \( h \)): \( \text{Area} = \frac{1}{2} \cdot c \cdot h \)
Steps:
- Input side \( a \), angle \( \alpha \), and angle \( \beta \) in degrees.
- Validate inputs: ensure \( a > 0 \), \( \alpha > 0 \), \( \beta > 0 \), and \( \alpha + \beta < 180^\circ \).
- Calculate the third angle \( \gamma \).
- Use the Law of Sines to find sides \( b \) and \( c \).
- Compute the height \( h \) using side \( a \) and angle \( \gamma \).
- Calculate the area using base \( c \) and height \( h \).
- Display results with angles rounded to 2 decimal places and lengths/areas to 4 decimal places.
3. Importance of AAS Triangle Calculations
AAS triangle calculations are essential for:
- Geometry: Fully defining a triangle’s dimensions when two angles and a non-included side are known, ensuring congruence with another triangle having the same AAS properties.
- Engineering: Designing structures with triangular components where angles are measured, and a reference side is known.
- Navigation: Solving problems involving angular measurements and a known distance, such as in triangulation.
4. Using the Calculator
Examples:
- Example 1: Side \( a = 16 \), \( \alpha = 40^\circ \), \( \beta = 25^\circ \)
\( \gamma = 180^\circ - 40^\circ - 25^\circ = 115.00^\circ \)
Side \( b = 16 \cdot \frac{\sin(25^\circ)}{\sin(40^\circ)} \approx 10.5149 \)
Side \( c = 16 \cdot \frac{\sin(115^\circ)}{\sin(40^\circ)} \approx 22.5235 \)
Height \( h = 16 \cdot \sin(115^\circ) \approx 14.5048 \)
Area \( = \frac{1}{2} \cdot 22.5235 \cdot 14.5048 \approx 163.3467 \).
- Example 2: Side \( a = 10 \), \( \alpha = 30^\circ \), \( \beta = 60^\circ \)
\( \gamma = 180^\circ - 30^\circ - 60^\circ = 90.00^\circ \)
Side \( b = 10 \cdot \frac{\sin(60^\circ)}{\sin(30^\circ)} \approx 17.3205 \)
Side \( c = 10 \cdot \frac{\sin(90^\circ)}{\sin(30^\circ)} = 20.0000 \)
Height \( h = 10 \cdot \sin(90^\circ) = 10.0000 \)
Area \( = \frac{1}{2} \cdot 20 \cdot 10 = 100.0000 \).
- Example 3: Side \( a = 5 \), \( \alpha = 45^\circ \), \( \beta = 45^\circ \)
\( \gamma = 180^\circ - 45^\circ - 45^\circ = 90.00^\circ \)
Side \( b = 5 \cdot \frac{\sin(45^\circ)}{\sin(45^\circ)} = 5.0000 \)
Side \( c = 5 \cdot \frac{\sin(90^\circ)}{\sin(45^\circ)} \approx 7.0711 \)
Height \( h = 5 \cdot \sin(90^\circ) = 5.0000 \)
Area \( = \frac{1}{2} \cdot 7.0711 \cdot 5 \approx 17.6778 \).
5. Frequently Asked Questions (FAQ)
Q: What does AAS mean in triangle calculations?
A: AAS stands for Angle-Angle-Side, meaning two angles and a non-included side are known. This configuration uniquely defines a triangle’s shape and scale.
Q: Why must the sum of the two angles be less than 180 degrees?
A: The sum of all three angles in a triangle must be 180 degrees. If the first two angles sum to 180 degrees or more, the third angle would be 0 or negative, which is not possible.
Q: Can I calculate the area of an AAS triangle?
A: Yes, once all sides and angles are determined, the area can be calculated using the base-height formula or directly using the AAS area formula involving sines of the angles.
 Home
Home
 Back
Back