AAA Triangle Calculator

1. What is an AAA Triangle Calculator?

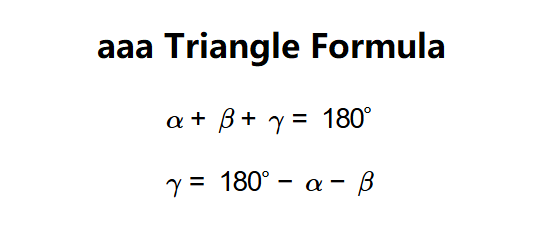
Definition: This calculator determines the missing angle in a triangle when two angles are known, using the fact that the sum of angles in a triangle is always 180 degrees. An AAA triangle refers to a triangle where only the three angles (\( \alpha \), \( \beta \), \( \gamma \)) are specified, defining the shape but not the size of the triangle.

Purpose: It aids in geometry education by helping users understand the relationship between angles in a triangle. It’s particularly useful for studying triangle properties and similarity, though it cannot determine side lengths or area without additional information.

2. How Does the Calculator Work?

The calculator uses the angle sum property of a triangle:

Sum of Angles: \( \alpha + \beta + \gamma = 180^\circ \)
Third Angle: \( \gamma = 180^\circ - \alpha - \beta \)

Steps:

Input the two known angles \( \alpha \) and \( \beta \) in degrees.
Validate inputs: ensure angles are positive and their sum is less than 180 degrees.
Calculate the third angle \( \gamma \) using the formula above.
Display the result rounded to 2 decimal places.

3. Importance of AAA Triangle Calculations

AAA triangle calculations are essential for:

Geometry Education: Understanding the fundamental property that the angles of a triangle always sum to 180 degrees.
Triangle Similarity: Determining if two triangles are similar by comparing their angles, as AAA triangles have the same shape but not necessarily the same size.
Design and Art: Ensuring proportional shapes in designs or models where only angles are specified.

4. Using the Calculator

Examples:

Example 1: Angles \( \alpha = 30^\circ \), \( \beta = 90^\circ \)
Third angle: \( \gamma = 180^\circ - 30^\circ - 90^\circ = 60.00^\circ \).
Example 2: Angles \( \alpha = 45^\circ \), \( \beta = 45^\circ \)
Third angle: \( \gamma = 180^\circ - 45^\circ - 45^\circ = 90.00^\circ \). This forms a right triangle.
Example 3: Angles \( \alpha = 60^\circ \), \( \beta = 60^\circ \)
Third angle: \( \gamma = 180^\circ - 60^\circ - 60^\circ = 60.00^\circ \). This forms an equilateral triangle shape.

5. Frequently Asked Questions (FAQ)

Q: What does AAA mean in triangle calculations?
A: AAA stands for Angle-Angle-Angle, meaning only the three angles of the triangle are known. It defines the shape but not the size of the triangle.

Q: Can I calculate the side lengths of an AAA triangle?
A: No, AAA triangles cannot be solved for side lengths because the angles only determine the shape, not the scale. You need at least one side length to compute the others.

Q: Why must the sum of the first two angles be less than 180 degrees?
A: The sum of all three angles in a triangle must be exactly 180 degrees. If the first two angles sum to 180 degrees or more, the third angle would be 0 or negative, which is not possible in a triangle.