A+Bi Form Calculator

1. What is an A+Bi Form Calculator?

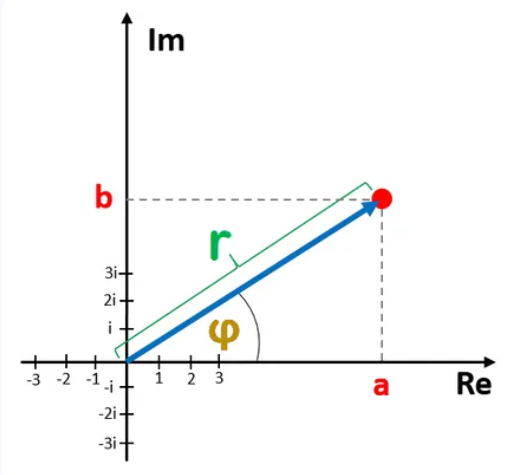
Definition: This calculator converts a complex number between its rectangular form (\( a + bi \), where \( a \) is the real part and \( b \) is the imaginary part) and polar form (\( r \exp(i\phi) \), where \( r \) is the magnitude and \( \phi \) is the phase in degrees). It handles conversions in both directions.

Purpose: It aids in mathematics, engineering, and physics by simplifying the representation of complex numbers, useful for applications like signal processing, electrical engineering, and quantum mechanics where complex numbers are common.

2. How Does the Calculator Work?

The calculator uses the following conversion formulas:

Polar to Rectangular (\( r \exp(i\phi) \to a + bi \)):

Real part: \( a = r \cos(\phi) \)
Imaginary part: \( b = r \sin(\phi) \)
Where \( \phi \) is in radians: \( \phi_{\text{rad}} = \phi \cdot \frac{\pi}{180} \)

Rectangular to Polar (\( a + bi \to r \exp(i\phi) \)):

Magnitude: \( r = \sqrt{a^2 + b^2} \)
Phase: \( \phi = \arctan2(b, a) \cdot \frac{180}{\pi} \)

Steps:

Select the conversion direction: Polar to Rectangular or Rectangular to Polar.
Input the required values.
Validate inputs: ensure magnitude is non-negative, and all inputs are valid numbers.
Apply the conversion formulas to compute the corresponding form.
Display results rounded to 3 decimal places.

3. Importance of A+Bi Form Calculations

Converting between rectangular and polar forms is essential for:

Electrical Engineering: Analyzing AC circuits, where complex numbers represent impedance (rectangular form) or phase shifts (polar form).
Signal Processing: Representing signals in the frequency domain, often using polar form for magnitude and phase.
Mathematics Education: Understanding complex numbers and their geometric interpretation in the complex plane.

4. Using the Calculator

Examples:

Polar to Rectangular: Magnitude \( r = 8 \), Phase \( \phi = 12^\circ \)
Convert \( \phi \) to radians: \( \phi_{\text{rad}} = 12 \cdot \frac{\pi}{180} \approx 0.2094 \)
Real part: \( a = 8 \cdot \cos(0.2094) \approx 7.825 \)
Imaginary part: \( b = 8 \cdot \sin(0.2094) \approx 1.663 \)
Result: \( 7.825 + 1.663i \).
Rectangular to Polar: Real part \( a = 3 \), Imaginary part \( b = 4 \)
Magnitude: \( r = \sqrt{3^2 + 4^2} = \sqrt{25} = 5.000 \)
Phase: \( \phi_{\text{rad}} = \arctan2(4, 3) \approx 0.9273 \), \( \phi = 0.9273 \cdot \frac{180}{\pi} \approx 53.130^\circ \)
Result: \( 5 \exp(i \cdot 53.130^\circ) \).
Special Case (Rectangular to Polar): Real part \( a = 0 \), Imaginary part \( b = 1 \)
Magnitude: \( r = \sqrt{0^2 + 1^2} = 1.000 \)
Phase: \( \phi_{\text{rad}} = \arctan2(1, 0) = \frac{\pi}{2} \), \( \phi = 90.000^\circ \)
Result: \( 1 \exp(i \cdot 90.000^\circ) \).

5. Frequently Asked Questions (FAQ)

Q: What is the difference between rectangular and polar forms?
A: The rectangular form (\( a + bi \)) expresses a complex number with a real part \( a \) and an imaginary part \( b \). The polar form (\( r \exp(i\phi) \)) expresses it with a magnitude \( r \) and phase angle \( \phi \), representing the number’s distance from the origin and angle in the complex plane.

Q: Why is the magnitude always non-negative?
A: The magnitude \( r \) is the distance from the origin in the complex plane, calculated as \( \sqrt{a^2 + b^2} \), which is always non-negative.

Q: What happens if both \( a \) and \( b \) are 0 in rectangular to polar conversion?
A: If \( a = 0 \) and \( b = 0 \), the magnitude \( r = 0 \), and the phase \( \phi \) is undefined. The calculator conventionally sets \( \phi = 0^\circ \).