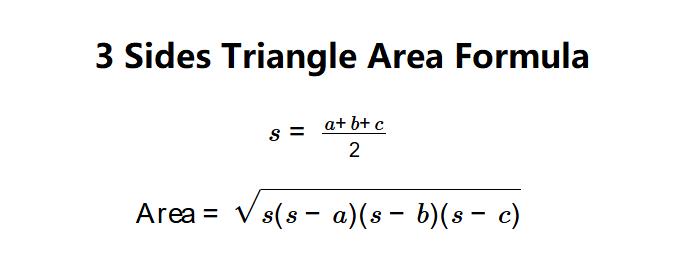3 Sides Triangle Area Calculator

Side \( a \):

Side \( b \):

Side \( c \):

1. What is a 3 Sides Triangle Area Calculator?

Definition: This calculator computes the area of a triangle using the lengths of its three sides \( a \), \( b \), and \( c \). It supports various length units (mm, cm, m, km, in, ft, yd) and area units (mm², cm², dm², m², km², in², ft², yd², mi²), with inputs defaulting to m and area output defaulting to m². It applies Heron's formula to calculate the area without needing the height of the triangle.

Purpose: It aids in geometry, architecture, and engineering by providing a quick way to determine the area of a triangle when only its side lengths are known, with flexible unit conversions for real-world applications like land surveying, design, and structural analysis.

2. How Does the Calculator Work?

The calculator uses Heron's formula to compute the area:

Semi-perimeter: \( s = \frac{a + b + c}{2} \)
Area: \( \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \)

Steps:

Input the lengths of the three sides \( a \), \( b \), and \( c \), with units defaulting to m.
Select the desired unit for the output area, defaulting to m².
Validate inputs: ensure all sides are positive and satisfy the triangle inequality in a consistent unit.
Convert all side lengths to meters for calculation.
Calculate the semi-perimeter \( s \).
Compute the area in square meters using Heron's formula.
Convert the area to the selected output unit.
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of 3 Sides Triangle Area Calculations

Calculating the area of a triangle using its three sides is essential for:

Geometry: Determining the area of any triangle (scalene, isosceles, or equilateral) without needing the height.
Land Surveying: Measuring the area of irregularly shaped plots of land in various units, such as m² or yd².
Engineering: Analyzing triangular components in structures, such as trusses, with measurements in units like m or ft.

4. Using the Calculator

Examples:

Scalene Triangle: Sides \( a = 3 \) m, \( b = 4 \) m, \( c = 5 \) m, Area in m²
Semi-perimeter: \( s = \frac{3 + 4 + 5}{2} = 6 \)
Area: \( \sqrt{6(6-3)(6-4)(6-5)} = \sqrt{36} = 6.0000 \) m².
Isosceles Triangle: Sides \( a = 0.5 \) m, \( b = 0.5 \) m, \( c = 0.6 \) m, Area in cm²
Semi-perimeter: \( s = \frac{0.5 + 0.5 + 0.6}{2} = 0.8 \)
Area in m²: \( \sqrt{0.8(0.8-0.5)(0.8-0.5)(0.8-0.6)} = \sqrt{0.0144} = 0.1200 \) m²
Convert to cm²: \( 0.1200 \times 10000 = 1200.0000 \) cm².
Equilateral Triangle: Sides \( a = 1.2192 \) m, \( b = 1.2192 \) m, \( c = 1.2192 \) m, Area in ft²
Semi-perimeter: \( s = \frac{1.2192 \times 3}{2} = 1.8288 \)
Area in m²: \( \sqrt{1.8288(1.8288-1.2192)^3} \approx 0.6440 \)
Convert to ft²: \( 0.6440 \times 10.7639104 \approx 6.9282 \) ft².

5. Frequently Asked Questions (FAQ)

Q: What is Heron's formula?
A: Heron's formula calculates the area of a triangle using its three side lengths: \( \text{Area} = \sqrt{s(s - a)(s - b)(s - c)} \), where \( s \) is the semi-perimeter, \( s = \frac{a + b + c}{2} \).

Q: Why do inputs default to m?
A: Meters (m) is the default unit for inputs to provide a standard metric base, ensuring consistency in calculations, but you can select other units like cm or ft as needed.

Q: Why does the area output default to m²?
A: Square meters (m²) is the default unit for the area output to align with the metric system, but you can convert it to other units like cm² or ft² using the dropdown.