2D Distance Calculator

1. What is a 2D Distance Calculator?

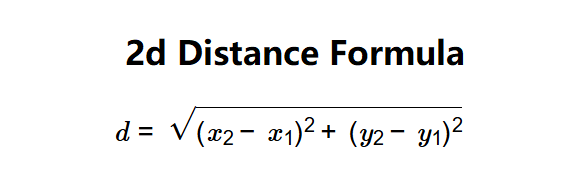
Definition: This calculator computes the straight-line distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \) in a 2D plane using the Euclidean distance formula. The distance represents the shortest path between the points, also known as the "as-the-crow-flies" distance.

Purpose: It aids in geometry, physics, computer graphics, and navigation by calculating distances in a 2D space, useful for applications like mapping, game development, and motion analysis.

2. How Does the Calculator Work?

The calculator uses the Euclidean distance formula:

Distance: \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \)

Steps:

Input the coordinates of the two points: \( (x_1, y_1) \) and \( (x_2, y_2) \).
Compute the differences: \( \Delta x = x_2 - x_1 \) and \( \Delta y = y_2 - y_1 \).
Calculate the distance using the formula: \( d = \sqrt{(\Delta x)^2 + (\Delta y)^2} \).
Format the output to 4 decimal places or scientific notation for very small or large values.

3. Importance of 2D Distance Calculations

2D distance calculations are essential for:

Geometry: Finding the length of a line segment or verifying properties of shapes like triangles.
Navigation: Calculating the straight-line distance between two locations on a map (e.g., for flight paths).
Computer Graphics: Determining distances between objects or points in 2D games or simulations.

4. Using the Calculator

Examples:

Simple Points: First point \( (x_1 = 0, y_1 = 0) \), Second point \( (x_2 = 3, y_2 = 4) \)
\( d = \sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5.0000 \).
Negative Coordinates: First point \( (x_1 = -1, y_1 = -2) \), Second point \( (x_2 = 2, y_2 = 2) \)
\( d = \sqrt{(2-(-1))^2 + (2-(-2))^2} = \sqrt{(3)^2 + (4)^2} = \sqrt{9 + 16} = 5.0000 \).
Decimal Coordinates: First point \( (x_1 = 1.5, y_1 = 2.5) \), Second point \( (x_2 = 4.5, y_2 = 6.5) \)
\( d = \sqrt{(4.5-1.5)^2 + (6.5-2.5)^2} = \sqrt{(3)^2 + (4)^2} = \sqrt{25} = 5.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What is the 2D distance formula?
A: The 2D distance formula, also known as the Euclidean distance, calculates the straight-line distance between two points \( (x_1, y_1) \) and \( (x_2, y_2) \): \( d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2} \).

Q: Can the coordinates be negative?
A: Yes, the coordinates can be any real numbers, including negative values, as the distance formula works with differences between coordinates.

Q: What if the two points are the same?
A: If the two points are the same (i.e., \( x_1 = x_2 \) and \( y_1 = y_2 \)), the distance will be 0, as there is no separation between them.