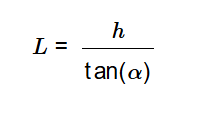1. What is the Shadow Length Calculator?

Definition: The Shadow Length Calculator computes the shadow length (\( L \)), object height (\( h \)), or sun elevation angle (\( \alpha \)) for a vertical object on a flat surface, based on the relationship between the object’s height and the sun’s position.

Purpose: It is used in architecture, solar energy, urban planning, and photography to design structures, position solar panels, or plan lighting and shading scenarios.

2. How Does the Calculator Work?

The calculator uses the following formulas based on the selected calculation mode:

Formulas:

• Shadow Length: \[ L = \frac{h}{\tan(\alpha)} \]
• Object Height: \[ h = L \cdot \tan(\alpha) \]
• Sun Elevation Angle: \[ \alpha = \arctan\left(\frac{h}{L}\right) \]

Where:

• \( L \): Shadow length (meters, centimeters, feet, inches, yards)
• \( h \): Object height (meters, centimeters, feet, inches, yards)
• \( \alpha \): Sun elevation angle (degrees, radians)

Unit Conversions:

• Length (\( L \), \( h \)):
  • 1 meter = 1 meter
  • 1 centimeter = 0.01 meters
  • 1 foot = 0.3048 meters
  • 1 inch = 0.0254 meters
  • 1 yard = 0.9144 meters
• Angle (\( \alpha \)):
  • 1 degree = 1 degree
  • 1 radian = \( \frac{180}{\pi} \) degrees

Steps:

• Select the variable to calculate: Shadow Length (\( L \)), Object Height (\( h \)), or Sun Elevation Angle (\( \alpha \)).
• Enter the required values with their units:
  • For \( L \): Enter \( h \) and \( \alpha \).
  • For \( h \): Enter \( L \) and \( \alpha \).
  • For \( \alpha \): Enter \( L \) and \( h \).
• Convert length inputs to meters and angle inputs to degrees.
• Calculate the result using the appropriate formula.
• Display the result:
  • For \( L \) or \( h \): In meters, centimeters, feet, inches, and yards with 4 decimal places.
  • For \( \alpha \): In degrees and radians with 4 decimal places.

3. Importance of Shadow Length Calculation

Calculating shadow-related variables is crucial for:

• Architecture and Urban Planning: Designing buildings to optimize natural light or shade.
• Solar Energy: Positioning solar panels to minimize shading.
• Photography: Planning shots based on shadow positions.
• Surveying: Estimating heights of objects using shadow measurements.

4. Using the Calculator

Example (Shadow Length): Calculate the shadow length of a 2-meter pole when the sun’s elevation angle is 30 degrees.

1. Select “Shadow Length (\( L \))”.
2. Enter \( h = 2 \), unit = Meters; \( \alpha = 30 \), unit = Degrees.
3. The calculator computes:
   • \( L = \frac{2}{\tan(30^\circ)} \approx \frac{2}{0.5774} \approx 3.464 \) meters
   • Convert: 346.4 cm, 11.3648 ft, 136.3776 in, 3.7817 yd
4. The calculator returns:
   • \( L \): 3.4640 m, 346.4000 cm, 11.3648 ft, 136.3776 in, 3.7817 yd

Example (Object Height): Calculate the height of a pole with a 3-meter shadow and a sun elevation angle of 45 degrees.

1. Select “Object Height (\( h \))”.
2. Enter \( L = 3 \), unit = Meters; \( \alpha = 45 \), unit = Degrees.
3. The calculator computes:
   • \( h = 3 \cdot \tan(45^\circ) = 3 \cdot 1 = 3 \) meters
   • Convert: 300 cm, 9.8425 ft, 118.1102 in, 3.2808 yd
4. The calculator returns:
   • \( h \): 3.0000 m, 300.0000 cm, 9.8425 ft, 118.1102 in, 3.2808 yd

Example (Sun Elevation Angle): Calculate the sun elevation angle for a 2-meter pole casting a 3.464-meter shadow.

1. Select “Sun Elevation Angle (\( \alpha \))”.
2. Enter \( L = 3.464 \), unit = Meters; \( h = 2 \), unit = Meters.
3. The calculator computes:
   • \( \alpha = \arctan\left(\frac{2}{3.464}\right) \approx \arctan(0.5774) \approx 30 \) degrees
   • Convert: \( 30 \cdot \frac{\pi}{180} \approx 0.5236 \) radians
4. The calculator returns:
   • \( \alpha \): 30.0000 deg, 0.5236 rad

5. Frequently Asked Questions (FAQ)

Q: What is shadow length?
A: Shadow length (\( L \)) is the distance of the shadow cast by a vertical object on a flat surface, determined by the object’s height (\( h \)) and the sun’s elevation angle (\( \alpha \)).

Q: How does the sun’s elevation angle affect shadow length?
A: A lower \( \alpha \) produces a longer shadow; a higher \( \alpha \) shortens it. At \( \alpha = 90^\circ \), no shadow is cast.

Q: What are some applications of this calculator?
A: It’s used in architecture, solar panel placement, photography, and surveying to manage light, shade, or estimate heights.

Shadow Length Calculator© - All Rights Reserved 2025