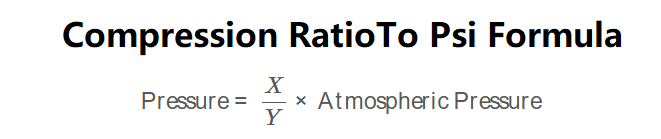Compression Ratio to PSI Calculator

Compression Ratio X:

Compression Ratio Y:

Atmospheric Pressure:

1. What is a Compression Ratio to PSI Calculator?

Definition: This calculator determines the pressure in an engine cylinder based on the compression ratio and atmospheric pressure.

Purpose: It is used in automotive engineering to estimate the cylinder pressure for engine design and performance analysis.

2. How Does the Calculator Work?

The calculator uses the following formula:

\[ \text{Pressure} = \frac{X}{Y} \times \text{Atmospheric Pressure} \] Where:

\(\text{Pressure}\): Calculated pressure (psi, bar, Pa, etc.)
\(X\): Compression ratio numerator (e.g., 9 in 9:1)
\(Y\): Compression ratio denominator (e.g., 1 in 9:1)
\(\text{Atmospheric Pressure}\): Standard atmospheric pressure (typically 14.7 psi)

Unit Conversions:

Atmospheric Pressure and Calculated Pressure:

1 bar = 14.5038 psi
1 Pa = 0.000145038 psi
1 at = 14.2233 psi
1 atm = 14.6959 psi
1 Torr = 0.0193368 psi
1 hPa = 0.0145038 psi
1 kPa = 0.145038 psi
1 MPa = 145.038 psi
1 GPa = 145038 psi
1 inHg = 0.491154 psi
1 mmHg = 0.0193368 psi

Steps:

Enter the compression ratio values \(X\) and \(Y\).
Enter the atmospheric pressure, selecting the unit (psi, bar, Pa, etc.).
Convert atmospheric pressure to psi if needed.
Calculate the pressure using the formula.
Convert the result to the selected pressure unit and display.

3. Importance of Compression Ratio to PSI Calculation

Calculating the pressure from the compression ratio is crucial for:

Engine Design: Determining cylinder pressures for material selection.
Performance Analysis: Understanding engine efficiency and power output.
Tuning: Optimizing compression ratios for specific fuel types.

4. Using the Calculator

Examples:

Example 1: For \(X = 10\), \(Y = 1\), \(\text{Atmospheric Pressure} = 14.7 \, \text{psi}\):
- Pressure: \(\text{Pressure} = \frac{10}{1} \times 14.7 = 147.00 \, \text{psi}\)
- In bar: \(\text{Pressure} = 147.00 \div 14.5038 = 10.13 \, \text{bar}\)
- In kPa: \(\text{Pressure} = 147.00 \div 0.145038 = 1013.25 \, \text{kPa}\)
Example 2: For \(X = 8\), \(Y = 1\), \(\text{Atmospheric Pressure} = 1.013 \, \text{bar}\):
- Convert: \(\text{Atmospheric Pressure} = 1.013 \times 14.5038 = 14.70 \, \text{psi}\)
- Pressure: \(\text{Pressure} = \frac{8}{1} \times 14.70 = 117.60 \, \text{psi}\)
- In atm: \(\text{Pressure} = 117.60 \div 14.6959 = 8.00 \, \text{atm}\)
- In mmHg: \(\text{Pressure} = 117.60 \div 0.0193368 = 6080.00 \, \text{mmHg}\)

5. Frequently Asked Questions (FAQ)

Q: What is compression ratio to PSI?
A: It calculates the pressure in an engine cylinder using the compression ratio and atmospheric pressure, with the formula \(\text{Pressure} = \frac{X}{Y} \times \text{Atmospheric Pressure}\).

Q: Can the compression ratio values be negative?
A: No, compression ratio values should be positive as negative values are not physically meaningful.

Q: What if the atmospheric pressure is zero?
A: If the atmospheric pressure is zero, the calculated pressure will also be zero, as there is no base pressure to multiply.

Favorite