2:12 Ramp Slope Calculator

Rise (Vertical Height):

Slope Ratio: Residential/Assisted User (2:12)

Recommend: Ramp Slope Calculator

Slope Angle:

Degrees (°)

Elevation Grade:

Percent (%)

Run (Horizontal Length):

Ramp Length:

Meters (m)

1. What is the Residential/Assisted User (2:12) Ramp Slope Calculator?

Definition: This calculator determines the slope angle, elevation grade, run, and ramp length for a ramp with a fixed 2:12 slope ratio, suitable for residential ramps or assisted wheelchair users.

Purpose: It assists homeowners, builders, and caregivers in designing ramps for residential settings or situations where assistance is available, allowing a steeper incline than ADA standards for public spaces.

2. How Does the Calculator Work?

The calculator uses the following equations for a 2:12 slope ratio (2 units rise per 12 units run, equivalent to 1:6):

Run: \( \text{Run} = \text{Rise} \times 6 \)
Ramp Length: \( L = \sqrt{\text{Rise}^2 + \text{Run}^2} \)
Slope Angle: \( \theta = \arctan\left(\frac{\text{Rise}}{\text{Run}}\right) \)
Elevation Grade: \( G = \frac{\text{Rise}}{\text{Run}} \times 100 \)

Where:

\( \text{Rise} \): Vertical height to overcome (cm, m, in, ft, or yd);
\( \text{Run} \): Horizontal length (m or ft);
\( L \): Ramp length, the hypotenuse (m or ft);
\( \theta \): Slope angle (degrees);
\( G \): Elevation grade (percent).

Steps:

Enter the rise and select its unit (cm, m, in, ft, or yd).
Convert rise to meters for calculations.
Calculate the run by multiplying rise by 6 (for 2:12 ratio).
Calculate the ramp length using the Pythagorean theorem.
Calculate the slope angle using arctangent.
Calculate the elevation grade as a percentage.
Convert run and ramp length to the selected output unit (m or ft).
Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Residential/Assisted User (2:12) Slope Calculation

Calculating the correct ramp dimensions for a 2:12 slope is critical for:

Accessibility: Provides a steeper but manageable incline for assisted wheelchair users or residential settings where space is limited.
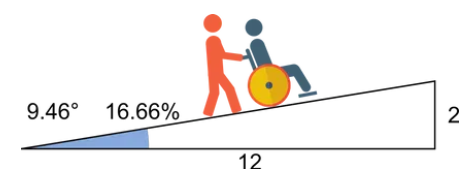
Safety: Maintains a slope of ~9.5° (16.67%) suitable for assisted use, balancing accessibility with practicality.
Flexibility: Allows steeper ramps in residential environments where ADA compliance is not required.

4. Using the Calculator

Example: Calculate the ramp parameters for a residential/assisted user slope:

Rise: \( 0.5 \, \text{m} \);
Slope Ratio: 2:12 (Residential/Assisted User);
Output Unit: Meters;
Run: \( 0.5 \times 6 = 3 \, \text{m} \);
Ramp Length: \( \sqrt{0.5^2 + 3^2} \approx 3.0414 \, \text{m} \);
Slope Angle: \( \arctan\left(\frac{0.5}{3}\right) \approx 9.4623^\circ \);
Elevation Grade: \( \frac{0.5}{3} \times 100 \approx 16.6667\% \);
Result: \( \theta = 9.4623^\circ, G = 16.6667\%, \text{Run} = 3.0000 \, \text{m}, L = 3.0414 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What does the 2:12 slope ratio mean?
A: A 2:12 ratio means 2 units of rise per 12 units of run (or 1:6), resulting in a slope of approximately 9.5° or 16.67%, suitable for residential ramps or assisted wheelchair users.

Q: Is the 2:12 slope ADA-compliant?
A: No, 2:12 is steeper than the ADA maximum of 1:12 for unassisted users. It is appropriate for residential settings or assisted users where ADA standards do not apply.

Q: Does the calculator account for ramp landings?
A: No, it calculates the straight ramp segment. Landings may be needed for longer ramps, depending on local building codes or user needs.