1:20 Ramp Slope Calculator

Rise (Vertical Height):

Slope Ratio: Unassisted user, ADA minimum slope (1:20)

Recommend: Ramp Slope Calculator

Slope Angle:

Degrees (°)

Elevation Grade:

Percent (%)

Run (Horizontal Length):

Ramp Length:

Meters (m)

1. What is the ADA Minimum Slope (1:20) Ramp Calculator?

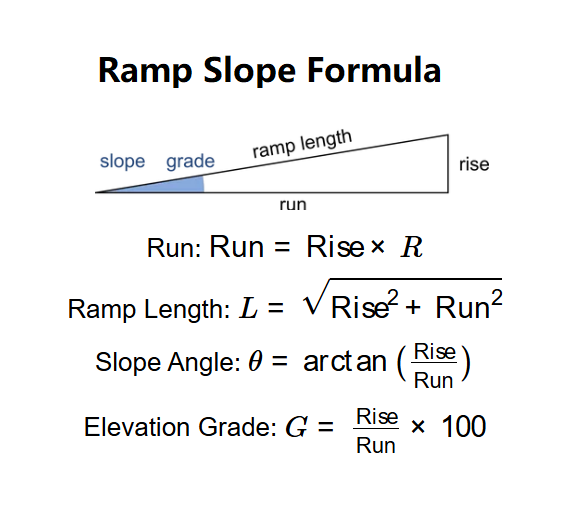
Definition: This calculator determines the slope angle, elevation grade, run, and ramp length for a ramp with a fixed 1:20 slope ratio, recommended by the Americans with Disabilities Act (ADA) as the gentlest slope for unassisted wheelchair users.

Purpose: It assists architects, builders, and individuals in designing ADA-compliant ramps that provide the easiest incline for maximum accessibility in public and commercial spaces.

2. How Does the Calculator Work?

The calculator uses the following equations for a 1:20 slope ratio (1 unit rise per 20 units run):

Run: \( \text{Run} = \text{Rise} \times 20 \)
Ramp Length: \( L = \sqrt{\text{Rise}^2 + \text{Run}^2} \)
Slope Angle: \( \theta = \arctan\left(\frac{\text{Rise}}{\text{Run}}\right) \)
Elevation Grade: \( G = \frac{\text{Rise}}{\text{Run}} \times 100 \)

Where:

\( \text{Rise} \): Vertical height to overcome (cm, m, in, ft, or yd);
\( \text{Run} \): Horizontal length (m or ft);
\( L \): Ramp length, the hypotenuse (m or ft);
\( \theta \): Slope angle (degrees);
\( G \): Elevation grade (percent).

Steps:

Enter the rise and select its unit (cm, m, in, ft, or yd).
Convert rise to meters for calculations.
Calculate the run by multiplying rise by 20 (for 1:20 ratio).
Calculate the ramp length using the Pythagorean theorem.
Calculate the slope angle using arctangent.
Calculate the elevation grade as a percentage.
Convert run and ramp length to the selected output unit (m or ft).
Display results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of ADA Minimum Slope (1:20) Calculation

Calculating the correct ramp dimensions for a 1:20 slope is critical for:

Accessibility: Provides the gentlest incline for unassisted wheelchair users, maximizing ease of use per ADA recommendations.
Safety: Maintains a slope of ~2.9° (5%) to minimize effort and ensure safety.
Compliance: Meets ADA guidelines and building codes for accessible ramps in public spaces.

4. Using the Calculator

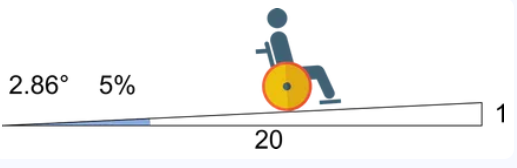
Example: Calculate the ramp parameters for an ADA minimum slope:

Rise: \( 0.5 \, \text{m} \);
Slope Ratio: 1:20 (ADA minimum slope);
Output Unit: Meters;
Run: \( 0.5 \times 20 = 10 \, \text{m} \);
Ramp Length: \( \sqrt{0.5^2 + 10^2} \approx 10.0125 \, \text{m} \);
Slope Angle: \( \arctan\left(\frac{0.5}{10}\right) \approx 2.8624^\circ \);
Elevation Grade: \( \frac{0.5}{10} \times 100 = 5\% \);
Result: \( \theta = 2.8624^\circ, G = 5.0000\%, \text{Run} = 10.0000 \, \text{m}, L = 10.0125 \, \text{m} \).

5. Frequently Asked Questions (FAQ)

Q: What does the 1:20 slope ratio mean?
A: A 1:20 ratio means 1 unit of rise per 20 units of run, resulting in a slope of approximately 2.9° or 5%, recommended by ADA as the gentlest incline for unassisted wheelchair users.

Q: Does the calculator account for ramp landings?
A: No, it calculates the straight ramp segment. For ramps longer than 30 feet (9.14 m) under ADA, landings (minimum 60 in or 1.525 m long) must be added separately.

Q: Why is the 1:20 ratio considered the minimum slope?
A: The 1:20 ratio is the gentlest slope recommended by ADA, offering the easiest incline for unassisted wheelchair users, ideal for accessibility in public and commercial settings where space allows.