Sum of Squares Calculator

1. What is the Sum of Squares Calculator?

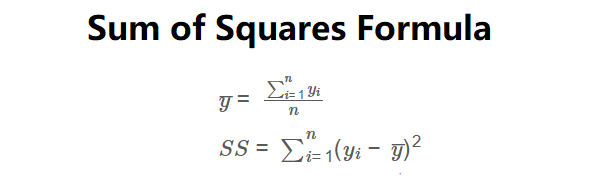
Definition: The Sum of Squares Calculator computes the sum of squared deviations (\( SS \)) from the sample mean, which measures the total variability in a dataset.

Purpose: This tool is used in statistics to quantify variability, serving as a building block for variance, standard deviation, and other analyses like ANOVA.

2. How Does the Calculator Work?

The calculator uses the following formulas for a dataset with \( n \) observations:

\( \bar{y} = \frac{\sum_{i=1}^n y_i}{n} \)

\( SS = \sum_{i=1}^n (y_i - \bar{y})^2 \)

Steps:

Enter a comma-separated list of numbers (at least 1).
Calculate the sample mean (\( \bar{y} \)).
Compute the squared difference from the mean for each data point (\( (y_i - \bar{y})^2 \)).
Sum the squared differences to get the sum of squares (\( SS \)).
Display the sample mean and sum of squares, formatted to four decimal places or scientific notation.

3. Importance of Sum of Squares

The sum of squares is critical for:

Variability Measurement: Quantifies the total deviation of data points from the mean.
Statistical Analysis: Used in calculating variance, standard deviation, and in techniques like regression and ANOVA.
Data Interpretation: Higher values indicate greater variability in the dataset.

4. Using the Calculator

Example: Calculate the sum of squares for the dataset: [20, 22, 18].

Input: 20,22,18
Sample Mean: \( \bar{y} = (20 + 22 + 18) / 3 = 60 / 3 = 20 \)
Squared Differences: \( (20 - 20)^2 = 0 \), \( (22 - 20)^2 = 4 \), \( (18 - 20)^2 = 4 \)
Sum of Squares: \( SS = 0 + 4 + 4 = 8 \)
Result: Sample Mean: 20.0000, Sum of Squares: 8.0000

5. Frequently Asked Questions (FAQ)

Q: What does the sum of squares represent?
A: It measures the total squared deviation of data points from the mean, indicating dataset variability.

Q: Why is at least one data point required?
A: The sum of squares requires a mean to compute deviations, which can be defined with one data point (though variability is zero in such cases).

Q: How is the sum of squares used in statistics?
A: It’s a key component in calculating variance, standard deviation, and in analyses like regression and ANOVA to assess data spread.