Standard Deviation of Sample Mean Calculator

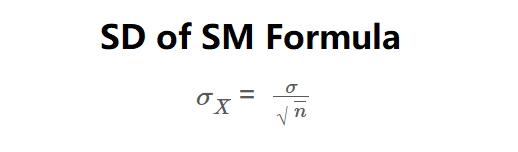
Standard Deviation of Sample Mean Formula

1. What is the Standard Deviation of Sample Mean Calculator?

Definition: The Standard Deviation of Sample Mean Calculator computes the standard deviation of the sample mean (\( \sigma_{\bar{X}} \)), which measures the variability of the sample mean as an estimate of the population mean.

Purpose: This tool is used in statistics to assess the precision of sample mean estimates, aiding in sampling design and inference.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( \sigma_{\bar{X}} = \frac{\sigma}{\sqrt{n}} \)

where \( \sigma \) is the population standard deviation and \( n \) is the sample size.

Steps:

Enter the population standard deviation (\( \sigma \)) and sample size (\( n \)).
Ensure the population standard deviation is non-negative and the sample size is a positive integer.
Calculate the standard deviation of the sample mean by dividing \( \sigma \) by the square root of \( n \).
Display the population standard deviation, sample size, and standard deviation of the sample mean, formatted to four decimal places or scientific notation (except for sample size, which is an integer).

3. Importance of Standard Deviation of Sample Mean

The standard deviation of the sample mean is critical for:

Precision Assessment: Indicates how close the sample mean is likely to be to the population mean.
Sampling Design: Helps determine the sample size needed to reduce estimation error.
Statistical Inference: Used in confidence intervals and hypothesis testing for population parameters.

4. Using the Calculator

Example: Calculate the standard deviation of the sample mean for a population standard deviation of 7.1 and a sample size of 100.

Input: Population Standard Deviation: 7.1, Sample Size: 100
Standard Deviation of Sample Mean: \( \sigma_{\bar{X}} = \frac{7.1}{\sqrt{100}} = \frac{7.1}{10} = 0.71 \)
Result: Population Standard Deviation: 7.1000, Sample Size: 100, Standard Deviation of Sample Mean: 0.7100

5. Frequently Asked Questions (FAQ)

Q: What does the standard deviation of the sample mean indicate?
A: It measures the variability of the sample mean as an estimate of the population mean, with smaller values indicating higher precision.

Q: Why must the sample size be a positive integer?
A: Sample size represents the number of observations, which must be a positive whole number for meaningful statistical calculations.

Q: How can the standard deviation of the sample mean be reduced?
A: Increasing the sample size (\( n \)) reduces \( \sigma_{\bar{X}} \), as it divides the population standard deviation by a larger square root.