Spearman's Rank Correlation Calculator

1. What is the Spearman's Rank Correlation Calculator?

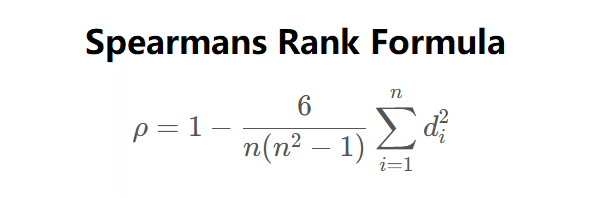
Definition: The Spearman's Rank Correlation Calculator computes Spearman's rank correlation coefficient (\( \rho \)), which measures the strength and direction of the monotonic relationship between two variables based on their ranks.

Purpose: This tool is used in statistics to assess non-linear but monotonic relationships, useful in fields like social sciences, biology, and finance when data may not meet Pearson’s linearity assumptions.

2. How Does the Calculator Work?

The calculator uses the simplified formula for Spearman's rank correlation:

\( \rho = 1 - \frac{6 \sum d_i^2}{N (N^2 - 1)} \)

where \( d_i \) is the difference between the ranks of corresponding \( X \) and \( Y \) values, and \( N \) is the number of data points.

Steps:

Enter two comma-separated lists of numbers for X and Y (equal length, at least 2 values).
Assign ranks to each value in X and Y, averaging ranks for ties.
Calculate the differences \( d_i \) between the ranks of corresponding X and Y values.
Compute the sum of squared differences \( \sum d_i^2 \).
Apply the formula to compute \( \rho \).
Display \( \rho \), formatted to four decimal places or scientific notation.

3. Importance of Spearman's Rank Correlation

Spearman's rank correlation is critical for:

Monotonic Relationships: Measures the strength of monotonic (not necessarily linear) relationships between variables.
Non-Parametric Analysis: Suitable for non-normal or ordinal data, unlike Pearson’s correlation.
Robustness to Outliers: Less sensitive to extreme values due to rank-based calculation.

4. Using the Calculator

Example: Calculate Spearman’s rank correlation for X: [1, 3, 3, 5] and Y: [1, 2, 3, 4].

Input: X: 1,3,3,5; Y: 1,2,3,4
Ranks X: [1, 2.5, 2.5, 4] (tie at 3 gets average of ranks 2 and 3)
Ranks Y: [1, 2, 3, 4]
Differences: \( d_i = [1-1, 2.5-2, 2.5-3, 4-4] = [0, 0.5, -0.5, 0] \)
Sum of Squared Differences: \( \sum d_i^2 = 0^2 + 0.5^2 + (-0.5)^2 + 0^2 = 0.5 \)
Spearman’s \( \rho \): \( 1 - \frac{6 \times 0.5}{4 \times (16 - 1)} = 1 - \frac{3}{60} = 0.95 \)
Result: Spearman's Rank Correlation: 0.9500

5. Frequently Asked Questions (FAQ)

Q: What does Spearman's rank correlation measure?
A: It measures the strength and direction of a monotonic relationship between two variables based on their ranks, ranging from -1 to 1.

Q: How does Spearman's differ from Pearson’s correlation?
A: Spearman’s uses ranks, making it suitable for non-linear monotonic relationships and non-normal data, while Pearson’s requires linear relationships and normality.

Q: How are ties handled in the calculation?
A: Ties are assigned the average of the ranks they would occupy, ensuring accurate correlation computation.