Simpson's Diversity Index Calculator

1. What is the Simpson's Diversity Index Calculator?

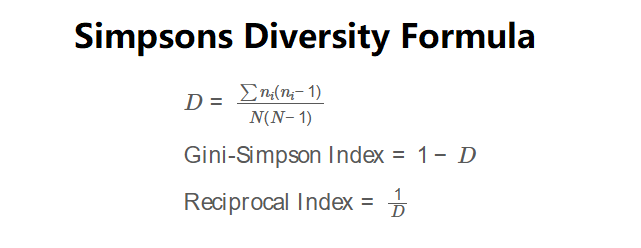
Definition: The Simpson's Diversity Index Calculator computes Simpson's Index (\( D \)), which measures the probability that two randomly selected individuals belong to the same species, the Gini-Simpson Index (\( 1-D \)), which measures the probability they belong to different species, and the Reciprocal Index (\( 1/D \)), which estimates the effective number of species.

Purpose: This tool quantifies biodiversity in ecological communities or diversity in other contexts (e.g., organizational diversity), accounting for both species richness and evenness.

2. How Does the Calculator Work?

The calculator uses the following formulas for a community with \( N \) total individuals and \( n_i \) individuals per species:

\( D = \frac{\sum n_i (n_i - 1)}{N (N - 1)} \)

\( \text{Gini-Simpson Index} = 1 - D \)

\( \text{Reciprocal Index} = \frac{1}{D} \)

Steps:

Enter a comma-separated list of species populations (at least 1).
Calculate the total number of individuals (\( N \)).
Compute \( \sum n_i (n_i - 1) \) for all species.
Calculate Simpson's Index (\( D \)) using the formula.
Compute the Gini-Simpson Index (\( 1-D \)) and Reciprocal Index (\( 1/D \)).
Display \( D \), \( 1-D \), and \( 1/D \), formatted to four decimal places or scientific notation.

3. Importance of Simpson's Diversity Index

Simpson’s indices are critical for:

Biodiversity Assessment: Quantifies species richness and evenness in ecological communities.
Comparative Analysis: Compares diversity across different communities or organizations.
Interdisciplinary Applications: Measures diversity in non-ecological contexts, such as gender or ethnic diversity in organizations.

4. Using the Calculator

Example: Calculate Simpson’s indices for species populations: [300, 335, 365].

Input: 300,335,365
Total Individuals: \( N = 300 + 335 + 365 = 1000 \)
\( N (N - 1) = 1000 \times 999 = 999,000 \)
Sum of \( n_i (n_i - 1) \): \( 300 \times 299 = 89,700 \), \( 335 \times 334 = 111,890 \), \( 365 \times 364 = 132,860 \), Total = \( 89,700 + 111,890 + 132,860 = 334,450 \)
Simpson's Index: \( D = \frac{334,450}{999,000} \approx 0.3348 \)
Gini-Simpson Index: \( 1 - D = 1 - 0.3348 = 0.6652 \)
Reciprocal Index: \( \frac{1}{D} = \frac{1}{0.3348} \approx 2.9869 \)
Result: Simpson's Index: 0.3348, Gini-Simpson Index: 0.6652, Reciprocal Index: 2.9869

5. Frequently Asked Questions (FAQ)

Q: What does Simpson's Index (\( D \)) represent?
A: It’s the probability that two randomly selected individuals from a community belong to the same species. A higher \( D \) indicates lower diversity.

Q: Why use the Gini-Simpson Index (\( 1-D \))?
A: It measures the probability that two individuals belong to different species, with higher values indicating greater diversity, making it more intuitive.

Q: What is the Reciprocal Index (\( 1/D \))?
A: It estimates the effective number of species, ranging from 1 to the number of species, with higher values indicating greater diversity.