Relative Standard Deviation Calculator

1. What is the Relative Standard Deviation Calculator?

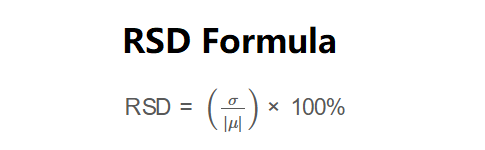
Definition: The Relative Standard Deviation (RSD) Calculator computes the RSD, which expresses the standard deviation as a percentage of the absolute mean, using user-provided mean and standard deviation values.

Purpose: This tool is used in statistics to measure relative variability, enabling comparison of precision across datasets with different scales or means.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( \text{RSD} = \left( \frac{\sigma}{|\mu|} \right) \times 100\% \)

where \( \mu \) is the mean and \( \sigma \) is the standard deviation.

Steps:

Enter the mean (\( \mu \)) and standard deviation (\( \sigma \)) of the dataset.
Ensure the standard deviation is non-negative.
Calculate the RSD by dividing the standard deviation by the absolute mean and multiplying by 100.
Display the mean (± RSD) and standard deviation, formatted to four decimal places or scientific notation.

3. Importance of Relative Standard Deviation

The RSD is critical for:

Relative Variability: Allows comparison of variability across datasets with different means.
Quality Control: Used in fields like science and engineering to assess precision relative to the mean.
Data Interpretation: Provides a standardized measure of variability as a percentage.

4. Using the Calculator

Example: Calculate the RSD for a dataset with mean = 25 and standard deviation = 2.

Input: Mean: 25, Standard Deviation: 2
RSD: \( \left( \frac{2}{|25|} \right) \times 100 = 8\% \)
Result: Mean: 25.0000 ± 8.0000%, Standard Deviation: 2.0000

5. Frequently Asked Questions (FAQ)

Q: What is relative standard deviation?
A: RSD is the standard deviation expressed as a percentage of the absolute mean, indicating relative variability.

Q: Why is RSD undefined when the mean is zero?
A: RSD involves division by the absolute mean, which is undefined if the mean is zero.

Q: Why must the standard deviation be non-negative?
A: Standard deviation measures spread and cannot be negative, as it is derived from squared differences.