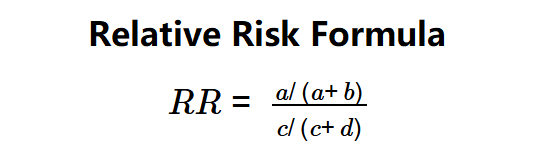Relative Risk Calculator

1. What is a Relative Risk Calculator?

Definition: This calculator determines the relative risk (RR) of developing a disease in an exposed group compared to a control group, including 95% confidence intervals.

Purpose: It assists in epidemiological studies and clinical research to assess the association between exposure and disease outcome.

2. How Does the Calculator Work?

The calculator uses the formula:

\( RR = \frac{a / (a + b)}{c / (c + d)} \)

Where:

\( a \): Number of exposed group members who developed the disease.
\( b \): Number of exposed group members who didn’t develop the disease.
\( c \): Number of control group members who developed the disease.
\( d \): Number of control group members who didn’t develop the disease.
\( RR \): Relative risk, a ratio comparing the risk in the exposed group to the control group.

Confidence Intervals:

\( \text{Lower Bound} = \exp[\ln(RR) - Z_c \times \sqrt{\frac{1}{a} + \frac{1}{c} - \frac{1}{a + b} - \frac{1}{c + d}}] \).
\( \text{Upper Bound} = \exp[\ln(RR) + Z_c \times \sqrt{\frac{1}{a} + \frac{1}{c} - \frac{1}{a + b} - \frac{1}{c + d}}] \).
\( Z_c = 1.96 \) for a 95% confidence interval.

Steps:

Input the number of members in each category (\( a \), \( b \), \( c \), \( d \)).
Validate: All values must be non-negative, and group totals must not be zero.
Calculate the relative risk ratio.
Compute the standard error and 95% confidence bounds using the updated formula.
Round to 4 decimal places and display the results.

3. Importance of Relative Risk Calculations

These calculations are key for:

Epidemiology: Identifying risk factors for diseases.
Clinical Trials: Evaluating treatment effects with uncertainty.
Public Health: Guiding prevention strategies.

4. Using the Calculator

Examples:

a = 80, b = 920, c = 10, d = 990 (e.g., heavy drinkers vs. control):
- \( \text{Risk Exposed} = 80 / 1000 = 0.0800 \).
- \( \text{Risk Control} = 10 / 1000 = 0.0100 \).
- \( RR = 0.0800 / 0.0100 = 8.0000 \).
- \( SE = \sqrt{\frac{1}{80} + \frac{1}{10} - \frac{1}{1000} - \frac{1}{1000}} \approx 0.1286 \).
- \( \text{Lower Bound} = e^{2.0794 - 1.96 \cdot 0.1286} \approx 5.6450 \).
- \( \text{Upper Bound} = e^{2.0794 + 1.96 \cdot 0.1286} \approx 11.3372 \).
- Result: RR = 8.0000, Lower CI = 5.6450, Upper CI = 11.3372.
a = 14, b = 42, c = 2, d = 83 (e.g., new medicine vs. placebo):
- \( \text{Risk Exposed} = 14 / 56 = 0.2500 \).
- \( \text{Risk Control} = 2 / 85 \approx 0.0235 \).
- \( RR = 0.2500 / 0.0235 \approx 10.6383 \).
- \( SE = \sqrt{\frac{1}{14} + \frac{1}{2} - \frac{1}{56} - \frac{1}{85}} \approx 0.4821 \).
- \( \text{Lower Bound} = e^{2.3646 - 1.96 \cdot 0.4821} \approx 3.3189 \).
- \( \text{Upper Bound} = e^{2.3646 + 1.96 \cdot 0.4821} \approx 34.1375 \).
- Result: RR = 10.6383, Lower CI = 3.3189, Upper CI = 34.1375.

5. Frequently Asked Questions (FAQ)

Q: What does RR = 1 mean?
A: It indicates equal risk between the exposed and control groups.

Q: What if a group total is zero?
A: The calculation is invalid, and an error is displayed.

Q: Why are confidence bounds asymmetric?
A: The logarithmic transformation ensures bounds are always positive, reflecting the ratio nature of RR.