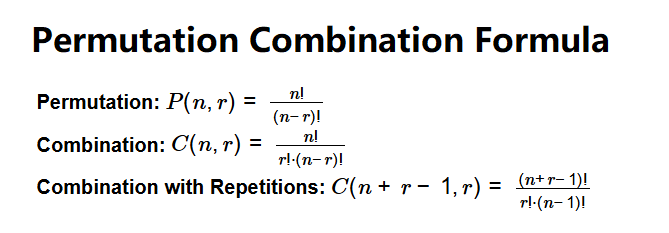1. What is a Permutation and Combination Calculator?

Definition: This calculator computes the number of ways to arrange or select items from a set, using permutations (\( P(n, r) \)) where order matters, combinations (\( C(n, r) \)) where order does not matter, or combinations with repetitions (\( C(n + r - 1, r) \)) where repetition is allowed.

Purpose: It supports combinatorics, probability calculations, and problem-solving in mathematics, statistics, and computer science.

2. How Does the Calculator Work?

The calculator uses these formulas:

• Permutation: \( P(n, r) = \frac{n!}{(n - r)!} \)
• Combination: \( C(n, r) = \frac{n!}{r! \cdot (n - r)!} \)
• Combination with Repetitions: \( C(n + r - 1, r) = \frac{(n + r - 1)!}{r! \cdot (n - 1)!} \)
• Where:
  • \( n \): Total number of item types.
  • \( r \): Number of items to choose or arrange.
  • \( ! \): Factorial (product of all positive integers up to that number).

Steps:

• Select calculation type: Permutation, Combination, or Combination with Repetitions.
• Input \( n \) (total items) and \( r \) (items to choose).
• Validate: \( n \geq 0 \), \( 0 \leq r \leq n \) for permutations/combinations, \( n \geq 1 \), \( r \geq 0 \) for combinations with repetitions, integers only.
• Compute \( P(n, r) \), \( C(n, r) \), or \( C(n + r - 1, r) \) using factorials.
• Display result with scientific notation if > 100,000 or < 0.0001, otherwise as an integer.

3. Importance of Permutation and Combination Calculations

These calculations are crucial for:

• Mathematics: Solving counting problems and probability scenarios.
• Computer Science: Algorithm design and data structure analysis.
• Statistics: Determining sample sizes and outcome possibilities.

4. Using the Calculator

Examples:

• Permutation (n = 9, r = 3):
  • \( P(9, 3) = \frac{9!}{(9 - 3)!} = \frac{9!}{6!} = 9 \cdot 8 \cdot 7 = 504 \).
  • Result: 504.
• Combination (n = 9, r = 3):
  • \( C(9, 3) = \frac{9!}{3! \cdot (9 - 3)!} = \frac{9!}{3! \cdot 6!} = \frac{9 \cdot 8 \cdot 7}{3 \cdot 2 \cdot 1} = 84 \).
  • Result: 84.
• Combination with Repetitions (n = 10, r = 3):
  • \( C(10 + 3 - 1, 3) = C(12, 3) = \frac{12!}{3! \cdot 9!} = \frac{12 \cdot 11 \cdot 10}{3 \cdot 2 \cdot 1} = 220 \).
  • Result: 220.
• Permutation (n = 20, r = 10):
  • \( P(20, 10) = \frac{20!}{10!} = 20 \cdot 19 \cdot 18 \cdot 17 \cdot 16 \cdot 15 \cdot 14 \cdot 13 \cdot 12 \cdot 11 = 670442572800 \).
  • Result: 6.70e11 (scientific notation due to > 100,000).

5. Frequently Asked Questions (FAQ)

Q: When is scientific notation used?
A: If the result is > 100,000 or < 0.0001, e.g., 6.70e11 for large permutations.

Q: What are combinations with repetitions?
A: They count ways to choose \( r \) items from \( n \) types with repetition allowed.

Q: Why limit \( r \leq n \) for some methods?
A: Permutations and combinations without repetition require \( r \leq n \), but repetitions allow \( r \) to exceed \( n \).

Permutation and Combination Calculator© - All Rights Reserved 2025