Pearson Correlation Calculator

1. What is the Pearson Correlation Calculator?

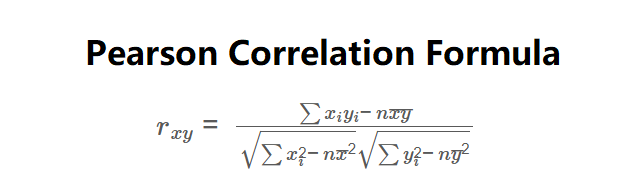
Definition: The Pearson Correlation Calculator computes the Pearson correlation coefficient (r), which measures the strength and direction of the linear relationship between two variables, X and Y.

Purpose: This tool is used in statistics to assess how well two datasets are linearly related, with values ranging from -1 (perfect negative correlation) to 1 (perfect positive correlation).

2. How Does the Calculator Work?

The calculator uses the following formula:

\( r_{xy} = \frac{\sum x_i y_i - n \bar{x} \bar{y}}{\sqrt{\sum x_i^2 - n \bar{x}^2} \sqrt{\sum y_i^2 - n \bar{y}^2}} \)

where \( x_i, y_i \) are the data points, \( \bar{x}, \bar{y} \) are the means, and \( n \) is the number of data points.

Steps:

Enter comma-separated lists of X and Y values (equal length, at least 2 values each).
Calculate the means of X and Y.
Compute the sum of products \( \sum x_i y_i \), and sums of squares \( \sum x_i^2, \sum y_i^2 \).
Calculate the numerator: \( \sum x_i y_i - n \bar{x} \bar{y} \).
Calculate the denominator: \( \sqrt{\sum x_i^2 - n \bar{x}^2} \sqrt{\sum y_i^2 - n \bar{y}^2} \).
Compute \( r \) as numerator divided by denominator, ensuring \( -1 \leq r \leq 1 \).
Display r, formatted to four decimal places or scientific notation.

3. Importance of Pearson Correlation

The Pearson correlation coefficient is essential for:

Relationship Analysis: Quantifies the strength and direction of linear relationships between variables.
Data Exploration: Helps identify patterns in datasets, useful in fields like finance, social sciences, and machine learning.
Model Validation: Assesses the linear fit in regression models.

4. Using the Calculator

Example: Calculate the Pearson correlation for X: [1, 3, 3, 5] and Y: [1, 2, 3, 4].

Input: X: 1,3,3,5; Y: 1,2,3,4
Mean X: \( \bar{x} = (1+3+3+5)/4 = 3 \)
Mean Y: \( \bar{y} = (1+2+3+4)/4 = 2.5 \)
Sums: \( \sum x_i y_i = 1 \cdot 1 + 3 \cdot 2 + 3 \cdot 3 + 5 \cdot 4 = 36 \)
\( \sum x_i^2 = 1^2 + 3^2 + 3^2 + 5^2 = 44 \), \( \sum y_i^2 = 1^2 + 2^2 + 3^2 + 4^2 = 30 \)
Numerator: \( 36 - 4 \cdot 3 \cdot 2.5 = 6 \)
Denominator: \( \sqrt{44 - 4 \cdot 3^2} \cdot \sqrt{30 - 4 \cdot 2.5^2} = \sqrt{8} \cdot \sqrt{5} \approx 6.32 \)
Result: \( r = 6 / 6.32 \approx 0.9487 \)

5. Frequently Asked Questions (FAQ)

Q: What does the Pearson correlation coefficient indicate?
A: It measures the strength and direction of the linear relationship between two variables, with values from -1 (perfect negative) to 1 (perfect positive).

Q: Does a correlation of 0 mean no relationship?
A: No, it means no linear relationship. Non-linear relationships may exist. Independence implies \( r = 0 \), but the converse is only true for jointly normal variables.

Q: Why is at least 2 data points required?
A: Correlation measures relationships between pairs of points, so at least two points are needed to compute variance and covariance.