How to Calculate P-Value Using Integral

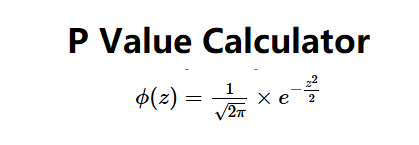
The p-value is the probability of observing a test statistic as extreme as the z-score under the null hypothesis. It is calculated by integrating the standard normal probability density function (PDF):

The cumulative distribution function (CDF), \( \Phi(z) \), is the integral of \( \phi(z) \) from \(-\infty\) to \( z \):

P-values are computed as:

• Two-Tailed Test: \( p = 2 \times (1 - \Phi(|z|)) \)
• Left-Tailed Test: \( p = \Phi(z) \)
• Right-Tailed Test: \( p = 1 - \Phi(z) \)

This calculator uses numerical integration (trapezoidal rule) to approximate \( \Phi(z) \). P-values less than 0.00001 are displayed in scientific notation.

Using the P-Value Calculator

This calculator computes the p-value for a z-score using the integral of the standard normal distribution. It is ideal for statistical hypothesis testing in research, data analysis, or education.

Input the z-score and select the test type. The calculator numerically integrates the PDF to estimate the CDF and computes the p-value, which can be compared to a significance level (e.g., 0.05).

Example: Calculate the p-value for a z-score of 1.96 in a two-tailed test.

1. Z-Score: \( 1.96 \)
2. Test Type: Two-Tailed
3. CDF: \( \Phi(1.96) \approx 0.975 \)
4. P-Value: \( 2 \times (1 - \Phi(1.96)) \approx 0.050 \)
5. Result: P-Value ≈ 0.050 (borderline significant at 0.05 level)

Use this tool for statistical analysis, A/B testing, or validating research hypotheses.

Common P-Value Table

The following table provides approximate p-values for common z-scores in a two-tailed test:

Z-Score	P-Value (Two-Tailed)
1.00	0.3174
1.96	0.0500
2.58	0.0098
3.00	0.0027

Use this table for quick reference or to verify calculator results.

Common FAQ

Below are frequently asked questions about P-Values:

• Q: Why use numerical integration?
  A: The standard normal PDF has no closed-form integral, so numerical methods like the trapezoidal rule approximate the CDF.
• Q: What does a p-value indicate?
  A: It indicates the probability of observing a z-score as extreme as the input, assuming the null hypothesis is true.
• Q: How accurate is this calculator?
  A: The trapezoidal rule with 1000 intervals provides high accuracy for most z-scores, with results rounded to 6 decimal places or scientific notation for small values.
• Q: When to use a left-tailed test?
  A: Use it when the alternative hypothesis predicts a decrease or lower value compared to the null hypothesis.