P-Hat Calculator

1. What is a P-Hat Calculator?

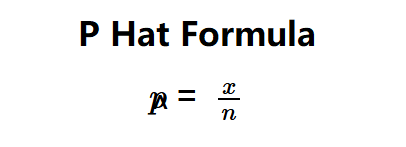
Definition: This calculator computes the sample proportion (\( \hat{p} \)), an estimate of the population proportion based on the number of occurrences in a sample.

Purpose: It assists in statistical inference, such as analyzing poll results or estimating event likelihoods from sample data.

2. How Does the Calculator Work?

The calculator uses the formula:

\( \hat{p} = \frac{x}{n} \)

Steps:

Input the number of occurrences and the sample size.
Validate: Occurrences ≥ 0, sample size ≥ 1, occurrences ≤ sample size.
Calculate \( \hat{p} = \frac{x}{n} \).
Convert to a percentage and round to 4 decimal places.
Display the result.

3. Importance of P-Hat Calculations

These calculations are key for:

Polls and Surveys: Estimating population preferences or opinions.
Hypothesis Testing: Supporting statistical inference about populations.
Quality Control: Assessing defect rates in manufacturing samples.

4. Using the Calculator

Examples:

Occurrences = 450, Sample Size = 700:
- \( \hat{p} = \frac{450}{700} \approx 0.6429 \).
- Result: 64.2900%.
Occurrences = 25, Sample Size = 60:
- \( \hat{p} = \frac{25}{60} \approx 0.4167 \).
- Result: 41.6700%.

5. Frequently Asked Questions (FAQ)

Q: What if occurrences exceed sample size?
A: The calculation is invalid, and an error is displayed.

Q: Why is \( \hat{p} \) a percentage?
A: It’s commonly expressed as a percentage for intuitive understanding in polls and reports.

Q: Can \( \hat{p} \) be greater than 1?
A: No, it’s constrained between 0 and 1 (or 0% to 100%).