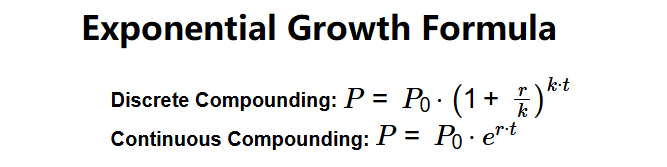1. What is Exponential Growth?

Definition: Exponential growth is a pattern where a quantity increases over time at a rate proportional to its current value, resulting in a rapidly rising curve.

Purpose: Used to model phenomena like population growth, compound interest, or website traffic growth when the rate remains relatively constant.

2. How Does the Calculator Work?

The calculator uses the following formulas, depending on compounding frequency:

• Discrete Compounding: \( P = P_0 \cdot \left(1 + \frac{r}{k}\right)^{k \cdot t} \)
• Continuous Compounding: \( P = P_0 \cdot e^{r \cdot t} \)
• \( P_0 \): Initial value, \( P \): Final value, \( r \): Growth rate (decimal), \( t \): Time (periods), \( k \): Compounding periods per unit time.

Derived Formulas:

• Time: \( t = \frac{\ln(P/P_0)}{k \cdot \ln(1 + r/k)} \) (discrete), \( t = \frac{\ln(P/P_0)}{r} \) (continuous)
• Growth Rate: \( r = k \cdot \left( \left( \frac{P}{P_0} \right)^{1/(k \cdot t)} - 1 \right) \) (discrete), \( r = \frac{\ln(P/P_0)}{t} \) (continuous)
• Initial Value: \( P_0 = \frac{P}{\left(1 + r/k\right)^{k \cdot t}} \) (discrete), \( P_0 = \frac{P}{e^{r \cdot t}} \) (continuous)

Steps:

• Select the calculation mode (e.g., Find Final Value).
• Enter the required inputs and compounding frequency.
• Click "Calculate" to compute the result.

3. When to Use Exponential Growth?

Use for:

• Modeling population growth, financial investments, or viral spread.
• Estimating future values or time to reach a goal when growth is constant.

4. Using the Calculator

Example: Initial value = 1000, growth rate = 5%, time = 10 years, annual compounding:

• Final Value: \( P = 1000 \cdot (1 + 0.05)^10 \approx 1628.8946 \).
• Time to reach 2000: \( t = \frac{\ln(2000/1000)}{\ln(1 + 0.05)} \approx 14.2067 \) years.
• Growth Rate to reach 2000 in 10 years: \( r = \left( (2000/1000)^{1/10} - 1 \right) \cdot 100 \approx 7.1773\% \).
• Initial Value to reach 2000 in 10 years at 5%: \( P_0 = 2000 / (1 + 0.05)^10 \approx 614.4579 \).

5. Frequently Asked Questions (FAQ)

Q: What is the difference between discrete and continuous compounding?
A: Discrete compounding applies growth at fixed intervals (e.g., annually), while continuous compounding assumes growth is applied instantaneously.

Q: Can the growth rate be negative?
A: Yes, a negative rate models exponential decay, but this calculator assumes positive growth.

Q: Why use scientific notation?
A: Values less than 0.0001 are displayed in scientific notation for readability.

Q: What if the growth rate isn’t constant?
A: The model assumes constant growth; for variable rates, consider logistic models or other tools.

Exponential Growth Prediction Calculator© - All Rights Reserved 2025