Conditional Probability Calculator

1. What is a Conditional Probability Calculator?

Definition: This calculator computes the conditional probability \( P(D|\oplus) \), the likelihood that a person is infected given a positive test result, using the relationship between joint and marginal probabilities.

Purpose: It supports probability analysis in medical diagnostics, decision-making, and statistics, particularly for assessing test accuracy in scenarios like early disease detection.

2. How Does the Calculator Work?

The calculator uses the following formulas:

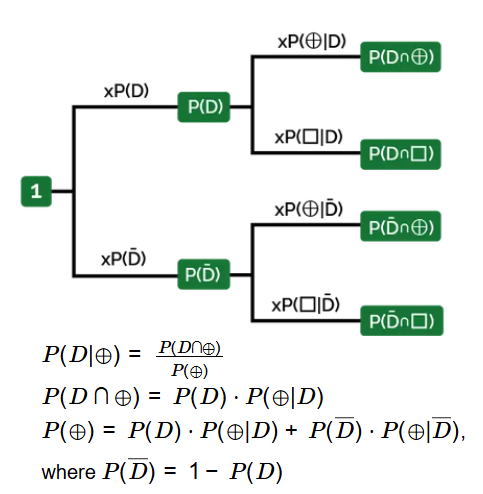
\( P(D|\oplus) = \frac{P(D \cap \oplus)}{P(\oplus)} \)
\( P(D \cap \oplus) = P(D) \cdot P(\oplus|D) \)
\( P(\oplus) = P(D) \cdot P(\oplus|D) + P(\overline{D}) \cdot P(\oplus|\overline{D}) \), where \( P(\overline{D}) = 1 - P(D) \)
Where:
- \( P(D) \): Probability of being infected.
- \( P(\oplus|D) \): Probability of a positive test given infection.
- \( P(\oplus|\overline{D}) \): Probability of a positive test given no infection.
- \( P(D \cap \oplus) \): Probability of being infected and testing positive.
- \( P(\oplus) \): Total probability of a positive test.

Steps:

Input \( P(D) \), \( P(\oplus|D) \), and \( P(\oplus|\overline{D}) \) as percentages.
Validate: All probabilities must be between 0% and 100%.
Convert to decimals for calculation.
Compute \( P(D \cap \oplus) = P(D) \cdot P(\oplus|D) \).
Compute \( P(\oplus) = P(D) \cdot P(\oplus|D) + (1 - P(D)) \cdot P(\oplus|\overline{D}) \).
Compute \( P(D|\oplus) = \frac{P(D \cap \oplus)}{P(\oplus)} \).
Convert to percentage and round to 4 decimal places.
Display the result, ensuring no division by zero.

3. Importance of Conditional Probability Calculations

These calculations are key for:

Medical Diagnostics: Evaluating the reliability of test results, e.g., COVID-19 antibody tests.
Statistics: Analyzing dependent events in data sets.
Decision-Making: Improving accuracy by considering patient conditions before testing.

4. Using the Calculator

Examples:

P(D) = 5%, P(⊕|D) = 91%, P(⊕|D̅) = 5%:
- \( P(D) = 0.05 \), \( P(\oplus|D) = 0.91 \), \( P(\oplus|\overline{D}) = 0.05 \).
- \( P(D \cap \oplus) = 0.05 \cdot 0.91 = 0.0455 \).
- \( P(\overline{D}) = 1 - 0.05 = 0.95 \).
- \( P(\oplus) = (0.05 \cdot 0.91) + (0.95 \cdot 0.05) = 0.0455 + 0.0475 = 0.093 \).
- \( P(D|\oplus) = \frac{0.0455}{0.093} \approx 0.4892 \).
- Result: 48.9200%.

5. Frequently Asked Questions (FAQ)

Q: What if P(⊕) is zero?
A: The calculation is undefined, and an error is displayed to avoid division by zero.

Q: Why use P(⊕|D) and P(⊕|D̅)?
A: They account for all possible states (infected or not) contributing to a positive test.

Q: How does this apply to real-world testing?
A: It helps assess test accuracy, e.g., in early pandemics, where low infection rates can lead to high false positives.