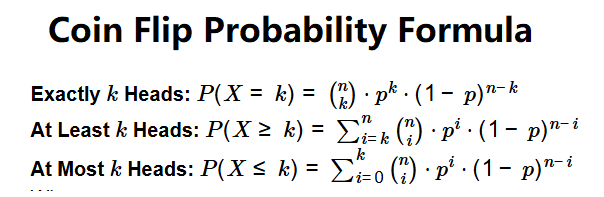Coin Flip Probability Calculator

1. What is a Coin Flip Probability Calculator?

Definition: This calculator computes the probability of getting exactly \( k \) heads, at least \( k \) heads, or at most \( k \) heads in \( n \) coin tosses, with a customizable probability of heads (\( p \)) for unfair coins.

Purpose: It supports probability education, statistical modeling, and analysis of random processes with binary outcomes.

2. How Does the Calculator Work?

The calculator uses the binomial probability formula:

Exactly \( k \) Heads: \( P(X = k) = \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k} \)
At Least \( k \) Heads: \( P(X \geq k) = \sum_{i=k}^{n} \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i} \)
At Most \( k \) Heads: \( P(X \leq k) = \sum_{i=0}^{k} \binom{n}{i} \cdot p^i \cdot (1 - p)^{n - i} \)
Where:
- \( n \): Number of tosses.
- \( k \): Number of heads.
- \( \binom{n}{k} = \frac{n!}{k! \cdot (n - k)!} \): Binomial coefficient.
- \( p \): Probability of heads (0 to 1).
- \( 1 - p \): Probability of tails.

Steps:

Select probability type: "Exactly \( k \) Heads", "At Least \( k \) Heads", or "At Most \( k \) Heads".
Input \( n \) (tosses), \( k \) (heads), and \( p \) (probability of heads in %).
Validate: \( n \geq 1 \), \( 0 \leq k \leq n \), \( 0 \leq p \leq 100 \), integers for \( n \) and \( k \).
For "Exactly": Compute \( \binom{n}{k} \cdot p^k \cdot (1 - p)^{n - k} \).
For "At Least": Sum from \( i = k \) to \( n \).
For "At Most": Sum from \( i = 0 \) to \( k \).
Convert to percentage for "Chance of Success"; use scientific notation if < 0.0001%.
Compute "Probability of 1 in" as \( 1 / P \), using scientific notation if \( P < 0.0001 \).
Display results.

3. Importance of Coin Flip Probability Calculations

These calculations are key for:

Statistics Education: Teaches binomial distributions with variable conditions.
Gambling Analysis: Evaluates outcomes with biased coins.
Random Processes: Models experiments with customizable success rates.

4. Using the Calculator

Examples:

Exactly 8 Heads in 10 Tosses (p = 50%):
- \( n = 10 \), \( k = 8 \), \( p = 0.5 \).
- \( \binom{10}{8} = 45 \).
- \( P(X = 8) = 45 \cdot (0.5)^8 \cdot (0.5)^2 = 45 / 1024 \approx 0.0439 \).
- Chance of Success: 4.3900%.
- Probability of 1 in: \( 1 / 0.0439 \approx 22.7790 \).
At Most 1 Head in 10 Tosses (p = 10%):
- \( n = 10 \), \( k = 1 \), \( p = 0.1 \).
- \( P(X \leq 1) = P(X = 0) + P(X = 1) \).
- \( P(X = 0) = \binom{10}{0} \cdot (0.1)^0 \cdot (0.9)^{10} \approx 1 \cdot 1 \cdot 0.3487 \approx 0.3487 \).
- \( P(X = 1) = \binom{10}{1} \cdot (0.1)^1 \cdot (0.9)^9 \approx 10 \cdot 0.1 \cdot 0.3874 \approx 0.3874 \).
- \( P(X \leq 1) \approx 0.3487 + 0.3874 = 0.7361 \).
- Chance of Success: 73.6100%.
- Probability of 1 in: \( 1 / 0.7361 \approx 1.3586 \).

5. Frequently Asked Questions (FAQ)

Q: What does At Most mean?
A: It calculates the probability of getting 0 to \( k \) heads, inclusive.

Q: When is scientific notation used?
A: For "Chance of Success" if \( P < 0.0001\% \) (e.g., 1.80e-14%), and for "1 in" if \( P < 0.0001 \).

Q: Can \( p \) be 100%?
A: Yes, but it trivializes results (e.g., \( k = n \) for "Exactly" gives 100%).