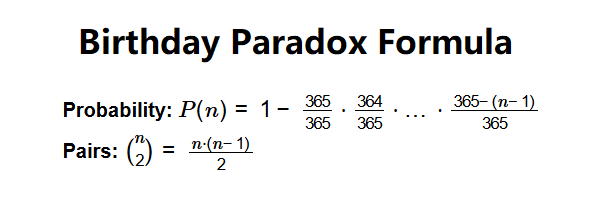Birthday Paradox Calculator - Probability and Pairs

1. What is a Birthday Paradox Calculator?

Definition: This calculator computes the probability that at least two people in a group of \( n \) share the same birthday and the number of possible pairs in the group. The birthday paradox shows that a 50% chance of a shared birthday occurs with just 23 people, due to the number of possible pairs.

Purpose: It illustrates probability concepts in statistics, with applications in cryptography (e.g., birthday attacks) and analyzing coincidences in datasets.

2. How Does the Calculator Work?

The calculator uses these formulas:

Probability: \( P(n) = 1 - \frac{365}{365} \cdot \frac{364}{365} \cdot \ldots \cdot \frac{365 - (n-1)}{365} \)
Pairs: \( \binom{n}{2} = \frac{n \cdot (n-1)}{2} \)
Where:
- \( n \): Number of people.
- \( P(n) \): Probability of at least two sharing a birthday.
- \( \binom{n}{2} \): Number of possible pairs.
- Leap years: Uses 365.25 days instead of 365.

Steps:

Input number of people (\( n \)).
Select leap year option (365 or 365.25 days).
Validate: \( n \) must be an integer between 1 and 1000.
Calculate probability of no shared birthdays: \( \frac{365}{365} \cdot \frac{364}{365} \cdot \ldots \cdot \frac{365 - (n-1)}{365} \).
Compute \( P(n) = 1 - \text{no shared probability} \).
Compute pairs: \( \frac{n \cdot (n-1)}{2} \).
Display probability (%) to 2 decimal places and pairs as an integer.

3. Importance of Birthday Paradox Calculations

These calculations are key for:

Statistics Education: Demonstrates surprising probability outcomes.
Cryptography: Informs birthday attack strategies for hash collisions.
Data Analysis: Estimates coincidence probabilities in large groups.

4. Using the Calculator

Example:

Group of 5 people, no leap years:
Probability: \( P(\text{no match}) = \frac{365}{365} \cdot \frac{364}{365} \cdot \frac{363}{365} \cdot \frac{362}{365} \cdot \frac{361}{365} \approx 0.9729 \).
\( P(5) = 1 - 0.9729 \approx 0.0271 \approx 2.71\% \).
Pairs: \( \binom{5}{2} = \frac{5 \cdot 4}{2} = 10 \).
Result: 2.71% chance of at least two sharing a birthday, 10 possible pairs.

5. Frequently Asked Questions (FAQ)

Q: Why is the birthday paradox surprising?
A: A 50% chance of a shared birthday occurs with only 23 people, far fewer than expected.

Q: Why calculate the number of pairs?
A: It shows why the probability grows quickly, as pairs increase quadratically with \( n \).

Q: How do leap years affect the result?
A: Using 365.25 days slightly increases the probability, requiring 367 people for 100% certainty.