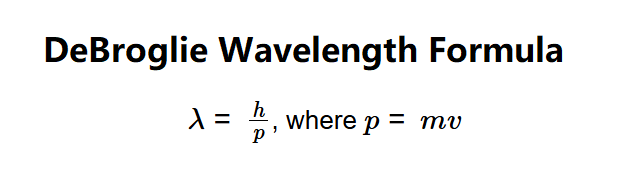de Broglie Wavelength Calculator

Mass of Particle (\( m \)):

Velocity of Particle (\( v \)):

1. What is the de Broglie Wavelength Calculator?

Definition: This calculator uses the de Broglie wavelength equation to compute the wavelength (\( \lambda \)) associated with a particle of mass \( m \) moving at velocity \( v \).

Purpose: It is used in quantum mechanics to illustrate the wave-particle duality of matter, showing that particles like electrons exhibit wave-like properties.

2. How Does the Calculator Work?

The calculator uses the following equation:

\( \lambda = \frac{h}{p} \), where \( p = m v \)

Where:

\( \lambda \): de Broglie wavelength (m, cm, mm, nm, pm, or Å);
\( h \): Planck's constant (\( 6.6261 \times 10^{-34} \, \text{J·s} \));
\( p \): Momentum (\( \text{kg·m/s} \));
\( m \): Mass of the particle (various units);
\( v \): Velocity of the particle (m/s, km/s, cm/s, mm/s).

Steps:

Enter the mass of the particle (\( m \)) with its unit.
Enter the velocity of the particle (\( v \)) with its unit.
Convert all inputs to base units (kg for \( m \), m/s for \( v \)).
Calculate the momentum: \( p = m \times v \).
Calculate the de Broglie wavelength: \( \lambda = \frac{h}{p} \).
Convert the wavelength to the selected output unit and display \( \lambda \), formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of de Broglie Wavelength Calculation

Calculating the de Broglie wavelength is crucial for:

Quantum Mechanics: Demonstrating the wave-particle duality of matter.
Electron Microscopy: Understanding the wave-like behavior of electrons in electron microscopes.
Particle Physics: Analyzing the behavior of particles at quantum scales.

4. Using the Calculator

Example 1: Calculate \( \lambda \) for an electron traveling at 1% of the speed of light:

Mass: \( m = 1 \, m_e = 9.10938356 \times 10^{-31} \, \text{kg} \);
Velocity: \( v = 0.01 \times 299792458 = 2,997,924.58 \, \text{m/s} \);
Momentum: \( p = m \times v = 9.10938356 \times 10^{-31} \times 2,997,924.58 \approx 2.7309245 \times 10^{-24} \, \text{kg·m/s} \);
Wavelength: \( \lambda = \frac{6.6261 \times 10^{-34}}{2.7309245 \times 10^{-24}} \approx 2.426 \times 10^{-10} \, \text{m} \);
Result: \( \lambda = 2.4260 \times 10^{-10} \, \text{m} \) or \( 0.2426 \, \text{nm} \).

Example 2 (Different Particle): Calculate \( \lambda \) for a proton traveling at 1 km/s:

Mass: \( m = 1 \, m_p = 1.6726219 \times 10^{-27} \, \text{kg} \);
Velocity: \( v = 1 \, \text{km/s} = 1000 \, \text{m/s} \);
Momentum: \( p = m \times v = 1.6726219 \times 10^{-27} \times 1000 \approx 1.6726219 \times 10^{-24} \, \text{kg·m/s} \);
Wavelength: \( \lambda = \frac{6.6261 \times 10^{-34}}{1.6726219 \times 10^{-24}} \approx 3.962 \times 10^{-10} \, \text{m} \);
Result: \( \lambda = 3.9620 \times 10^{-10} \, \text{m} \) or \( 0.3962 \, \text{nm} \).

5. Frequently Asked Questions (FAQ)

Q: What does the de Broglie wavelength represent?
A: It represents the wavelength associated with a particle's wave-like behavior, illustrating the quantum principle of wave-particle duality.

Q: Why does a higher velocity result in a smaller wavelength?
A: The de Broglie wavelength is inversely proportional to momentum (\( \lambda \propto \frac{1}{p} \)), and since \( p = m v \), a higher velocity increases momentum, reducing the wavelength.

Q: Is this calculator applicable for relativistic speeds?
A: This calculator uses the non-relativistic approximation (\( p = m v \)). For speeds close to the speed of light, relativistic effects must be considered, which this calculator does not account for.