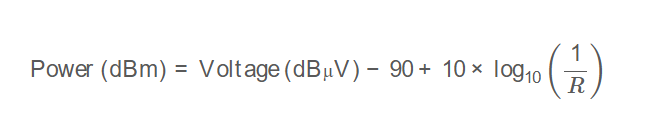dBµV to dBm Calculator

\( \text{Voltage (dBµV)} \): dBµV

\( R \): Ω

1. What is dBµV to dBm Calculator?

Definition: This calculator converts a voltage level in dBµV (decibels relative to 1 microvolt) to a power level in dBm (decibels relative to 1 milliwatt), taking into account the characteristic impedance of the system.

Purpose: It is used in RF engineering, telecommunications, and electronics to relate voltage measurements (often used in RF signal analysis) to power levels, which are critical for system design and performance evaluation.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ \text{Power (dBm)} = \text{Voltage (dBµV)} - 90 + 10 \times \log_{10}\left(\frac{1}{R}\right) \] Where:

\( \text{Power (dBm)} \): Power level in decibels relative to 1 milliwatt (dBm)
\( \text{Voltage (dBµV)} \): Voltage level in decibels relative to 1 microvolt (dBµV)
\( R \): Characteristic impedance (Ω)

Unit Conversions:

Voltage (dBµV): Measured in dBµV, no conversion needed
Impedance (R): Measured in ohms (Ω), no conversion needed
Power (dBm): Measured in dBm, no conversion needed

Steps:

Enter the voltage level in dBµV.
Enter the characteristic impedance (\( R \)) in ohms (default is 50 Ω, common in RF systems).
Calculate \( \text{Power (dBm)} = \text{Voltage (dBµV)} - 90 + 10 \times \log_{10}\left(\frac{1}{R}\right) \).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of dBµV to dBm Calculation

Calculating dBm from dBµV is crucial for:

RF Engineering: Converting voltage measurements (common in RF signal analysis) to power levels for system design and troubleshooting.
Telecommunications: Analyzing signal strength in receivers, antennas, and other RF equipment.
Electronics: Ensuring proper power matching in circuits with specific impedance values, such as in cable TV or radio systems.

4. Using the Calculator

Examples:

Example 1: For \( \text{Voltage (dBµV)} = 60 \, \text{dBµV} \), \( R = 50 \, \Omega \):
- \( \text{Power (dBm)} = 60 - 90 + 10 \times \log_{10}\left(\frac{1}{50}\right) \)
- \( \frac{1}{50} = 0.02 \)
- \( 10 \times \log_{10}(0.02) \approx -16.9897 \)
- \( \text{Power (dBm)} = 60 - 90 - 16.9897 \approx -46.9897 \, \text{dBm} \)
Example 2: For \( \text{Voltage (dBµV)} = 80 \, \text{dBµV} \), \( R = 75 \, \Omega \):
- \( \text{Power (dBm)} = 80 - 90 + 10 \times \log_{10}\left(\frac{1}{75}\right) \)
- \( \frac{1}{75} \approx 0.013333 \)
- \( 10 \times \log_{10}(0.013333) \approx -18.7506 \)
- \( \text{Power (dBm)} = 80 - 90 - 18.7506 \approx -28.7506 \, \text{dBm} \)

5. Frequently Asked Questions (FAQ)

Q: What is dBµV?
A: dBµV is a logarithmic measure of voltage relative to 1 microvolt, commonly used in RF and telecommunications to express small signal levels.

Q: Why does impedance matter in the conversion?
A: Impedance (\( R \)) affects the power calculation because power is proportional to the square of voltage divided by impedance (\( P = \frac{V^2}{R} \)).

Q: How is dBµV to dBm conversion used in real life?
A: It is used in RF measurements, such as in spectrum analyzers, to convert voltage levels of signals to power levels for system design, signal analysis, and compliance testing.