1. What is Young's Modulus and Shear Modulus Calculator?

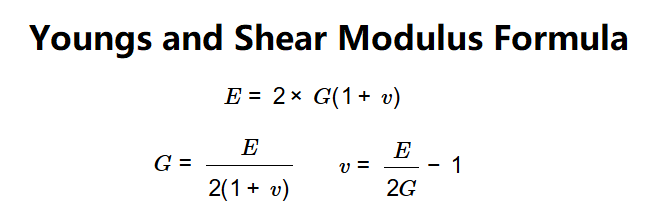
Definition: This calculator computes the relationship between Young's modulus (\( E \)), shear modulus (\( G \)), and Poisson's ratio (\( v \)) for isotropic and homogeneous materials, using the equation \( E = 2 \times G (1 + v) \).

Purpose: It is used in material science and engineering to determine one of these parameters when the other two are known, aiding in the design and analysis of materials under stress.

2. How Does the Calculator Work?

The calculator uses the following equation:

Formula: \[ E = 2 \times G (1 + v) \] Rearranged forms:

• Young's Modulus: \[ E = 2 \times G (1 + v) \]
• Shear Modulus: \[ G = \frac{E}{2 (1 + v)} \]
• Poisson's Ratio: \[ v = \frac{E}{2G} - 1 \]

Where:

• \( E \): Young's modulus (GPa, MPa, Pa, psi)
• \( G \): Shear modulus (GPa, MPa, Pa, psi)
• \( v \): Poisson's ratio (dimensionless)

Unit Conversions:

• Young's Modulus (\( E \)) and Shear Modulus (\( G \)):
  • 1 GPa = 1 GPa
  • 1 MPa = 10⁻³ GPa
  • 1 Pa = 10⁻⁹ GPa
  • 1 psi = 6.89476 × 10⁻³ GPa

Steps:

• Select the parameter to calculate (\( E \), \( G \), or \( v \)).
• Enter the values of the other two parameters with their respective units.
• Convert all inputs to GPa for calculation.
• Calculate the selected parameter using the appropriate formula.
• Convert the result to the selected unit (if applicable).
• Display the result with 4 decimal places.

3. Importance of Young's Modulus and Shear Modulus Calculation

Calculating these parameters is crucial for:

• Material Selection: Determining the stiffness and shear resistance of materials for engineering applications.
• Structural Analysis: Analyzing how materials deform under tensile and shear stresses in structures like beams, columns, and plates.
• Design Optimization: Ensuring materials meet the required mechanical properties for specific applications, such as in aerospace, automotive, and civil engineering.

4. Using the Calculator

Example: Calculate the Young's modulus (\( E \)) for a material with a shear modulus (\( G = 30 \, \text{GPa} \)) and Poisson's ratio (\( v = 0.3 \)).

1. Select "Calculate Young's Modulus (\( E \))".
2. Enter the shear modulus, \( G = 30 \, \text{GPa} \).
3. Enter the Poisson's ratio, \( v = 0.3 \).
4. The calculator computes \( E \):
   • \( E = 2 \times G (1 + v) \)
   • \( E = 2 \times 30 \times (1 + 0.3) \)
   • \( E = 2 \times 30 \times 1.3 = 78 \, \text{GPa} \)
5. The calculator returns \( E = 78.0000 \, \text{GPa} \).

5. Frequently Asked Questions (FAQ)

Q: What is the relationship between Young's modulus, shear modulus, and Poisson's ratio?
A: For isotropic and homogeneous materials, they are related by the equation \( E = 2 \times G (1 + v) \), where \( E \) is Young's modulus, \( G \) is the shear modulus, and \( v \) is Poisson's ratio.

Q: Why is Poisson's ratio typically between -1 and 0.5?
A: Poisson's ratio measures the lateral strain relative to the longitudinal strain. For most materials, it is positive (0 to 0.5), indicating that they contract laterally when stretched longitudinally. Negative values (down to -1) are possible for auxetic materials, which expand laterally when stretched.

Q: How are Young's modulus and shear modulus used in real life?
A: They are used in engineering to design materials and structures that can withstand tensile and shear stresses, such as in bridges, aircraft, and machinery, ensuring safety and performance under load.

Young's Modulus and Shear Modulus Calculator© - All Rights Reserved 2025