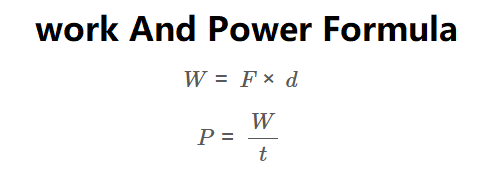Work and Power Calculator

Work Input Mode:

Work (W):

Force (F):

Distance (d):

Time (t):

Work (W):

Power (P):

1. What is a Work and Power Calculator?

Definition: This calculator determines the work done on an object and the power required to do that work over a period of time.

Purpose: It is used in physics to calculate energy transfer (work) and the rate of energy transfer (power).

2. How Does the Calculator Work?

The calculator uses the following formulas:

Work (if using force and distance): \[ W = F \times d \] Power: \[ P = \frac{W}{t} \] Where:

\( W \): Work done (J, kJ, MJ, Wh, kWh, ft-lb, kcal, eV)
\( F \): Force applied to the object (N, kN, MN, GN, TN)
\( d \): Distance the object moved (mm, cm, m, km, in, ft, yd, mi)
\( P \): Power (mW, W, kW, MW, GW, BTU/h, hp(I))
\( t \): Time (sec, min, hr, days, wks, mos, yrs)

Unit Conversions:

Force (F): N, kN (1 kN = 1000 N), MN (1 MN = 1000000 N), GN (1 GN = 1000000000 N), TN (1 TN = 1000000000000 N)
Distance (d): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Work (W): J, kJ (1 J = 0.001 kJ), MJ (1 J = 0.000001 MJ), Wh (1 J = 1/3600 Wh), kWh (1 J = 1/3600000 kWh), ft-lb (1 J = 0.73756214927727 ft-lb), kcal (1 J = 1/4184 kcal), eV (1 J = 1/1.60218e-19 eV)
Time (t): sec, min (1 min = 60 s), hr (1 hr = 3600 s), days (1 day = 86400 s), wks (1 wk = 604800 s), mos (1 mo = 2628000 s), yrs (1 yr = 31536000 s)
Power (P): mW (1 mW = 0.001 W), W, kW (1 kW = 1000 W), MW (1 MW = 1000000 W), GW (1 GW = 1000000000 W), BTU/h (1 BTU/h = 0.293071 W), hp(I) (1 hp(I) = 745.7 W)

Steps:

Select the work input mode (Direct Work Input or Input Force and Displacement).
Enter the work directly or calculate it using force and distance.
Enter the time and select its unit.
Convert work to Joules (J) and time to seconds (s).
Calculate power using \( P = \frac{W}{t} \).
Convert power to the selected unit and display both work and power.
If the result is less than 0.001, display it in scientific notation; otherwise, display it with 3 decimal places.

3. Importance of Work and Power Calculation

Calculating work and power is crucial for:

Physics Education: Understanding energy transfer and the rate of energy transfer.
Engineering: Designing systems that involve mechanical work and power.
Energy Analysis: Evaluating the efficiency of machines and systems.

4. Using the Calculator

Examples:

Example 1 (Direct Work Input): For \( W = 9000 \, \text{J} \), \( t = 60 \, \text{sec} \):
- Work: \( 9000.000 \, \text{J} \)
- Power: \( P = \frac{9000}{60} = 150.000 \, \text{W} \)
- In kW: \( P = 150 \times 0.001 = 0.150 \, \text{kW} \)
Example 2 (Force and Displacement): For \( F = 1000 \, \text{N} \), \( d = 9 \, \text{m} \), \( t = 1 \, \text{min} \):
- Work: \( W = 1000 \times 9 = 9000.000 \, \text{J} \)
- Time: \( t = 1 \times 60 = 60 \, \text{sec} \)
- Power: \( P = \frac{9000}{60} = 150.000 \, \text{W} \)
- In hp(I): \( P = 150 \times (1/745.7) = 0.201 \, \text{hp(I)} \)
Example 3 (Small Values with Scientific Notation): For \( W = 0.0001 \, \text{J} \), \( t = 100 \, \text{sec} \):
- Work: \( 1.000 \times 10^{-4} \, \text{J} \) (since 0.0001 < 0.001)
- Power: \( P = \frac{0.0001}{100} = 0.000001 = 1.000 \times 10^{-6} \, \text{W} \)
- In mW: \( P = 1.000 \times 10^{-6} \times 1000 = 1.000 \times 10^{-3} \, \text{mW} \)

5. Frequently Asked Questions (FAQ)

Q: What is power in physics?
A: Power is the rate at which work is done or energy is transferred, calculated as \( P = \frac{W}{t} \).

Q: What is the difference between work and power?
A: Work is the total energy transferred (\( W = F \times d \)), while power is the rate of doing work (\( P = \frac{W}{t} \)).

Q: Can power be negative?
A: In this calculator, power is assumed to be positive as work and time are positive. Negative power would occur if work were negative, indicating energy being removed.

Favorite