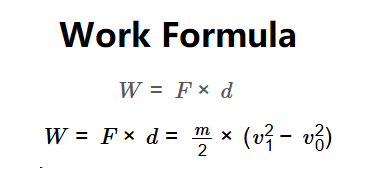Work Calculator

Work Calculator - Calculate Work from Velocity Change

Select Mode:

Force (F):

Distance (d):

Mass (m):

Initial Velocity (v₀):

Final Velocity (v₁):

Time (t):

1. What is a Work Calculator?

Definition: This calculator determines the work done on an object, either by applying a force over a distance or by changing its velocity.

Purpose: It is used in physics to calculate the energy transferred to an object when a force is applied.

2. How Does the Calculator Work?

The calculator supports two methods to calculate work:

1. Basic Work Formula: \[ W = F \times d \] 2. Work from Velocity Change:

Force: \( F = m \times a = m \times \frac{v_1 - v_0}{t} \)
Distance: \( d = t \times \frac{v_0 + v_1}{2} \)
Work: \( W = F \times d = \frac{m}{2} \times (v_1^2 - v_0^2) \)

Where:

\( W \): Work done (J, kJ, MJ, Wh, kWh, ft-lb, kcal)
\( F \): Force applied to the object (N, kN, MN, GN, TN)
\( d \): Distance the object moved (mm, cm, m, km, in, ft, yd, mi)
\( m \): Mass of the object (kg)
\( v_0 \): Initial velocity (m/s)
\( v_1 \): Final velocity (m/s)
\( t \): Time (s)

Unit Conversions:

Force (F): N, kN (1 kN = 1000 N), MN (1 MN = 1000000 N), GN (1 GN = 1000000000 N), TN (1 TN = 1000000000000 N)
Distance (d): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, km (1 km = 1000 m), in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m), mi (1 mi = 1609.344 m)
Mass (m): kg
Velocity (v₀, v₁): m/s
Time (t): s
Work (W): J, kJ (1 J = 0.001 kJ), MJ (1 J = 0.000001 MJ), Wh (1 J = 1/3600 Wh), kWh (1 J = 1/3600000 kWh), ft-lb (1 J = 0.73756214927727 ft-lb), kcal (1 J = 1/4184 kcal)

Steps:

Select the calculation mode (Basic Work Formula or Work from Velocity Change).
Enter the required values (force and distance, or mass, initial velocity, final velocity, and time) and select their units.
Convert all inputs to base units (N, m, kg, m/s, s) for calculation.
Calculate the work using the selected formula.
Convert the result to the selected energy unit and display.

3. Importance of Work Calculation

Calculating work is crucial for:

Physics Education: Understanding the concept of energy transfer.
Engineering: Designing systems that involve mechanical work.
Mechanics: Analyzing the motion of objects under applied forces.

4. Using the Calculator

Examples:

Example 1 (Basic Work Formula): For \( F = 10 \, \text{N} \), \( d = 5 \, \text{m} \):
- Work: \( W = 10 \times 5 = 50.000 \, \text{J} \)
- In kJ: \( W = 50 \times 0.001 = 0.050 \, \text{kJ} \)
Example 2 (Basic Work Formula with Units): For \( F = 1 \, \text{kN} \), \( d = 500 \, \text{cm} \):
- Convert: \( F = 1 \times 1000 = 1000 \, \text{N} \), \( d = 500 \times 0.01 = 5 \, \text{m} \)
- Work: \( W = 1000 \times 5 = 5000.000 \, \text{J} \)
- In ft-lb: \( W = 5000 \times 0.73756214927727 = 3687.811 \, \text{ft-lb} \)
Example 3 (Work from Velocity Change): For \( m = 2 \, \text{kg} \), \( v_0 = 0 \, \text{m/s} \), \( v_1 = 5 \, \text{m/s} \), \( t = 2 \, \text{s} \):
- Work: \( W = \frac{2}{2} \times (5^2 - 0^2) = 1 \times 25 = 25.000 \, \text{J} \)
- In kcal: \( W = 25 \times (1/4184) = 0.006 \, \text{kcal} \)

5. Frequently Asked Questions (FAQ)

Q: What is work in physics?
A: Work is the energy transferred to an object when a force is applied over a distance, calculated as \( W = F \times d \).

Q: Can work be negative?
A: Yes, work can be negative if the force and displacement are in opposite directions, but this calculator assumes positive inputs for simplicity.

Q: How does velocity change relate to work?
A: When an object changes velocity, the work done can be calculated using the change in kinetic energy, as shown in the formula \( W = \frac{m}{2} \times (v_1^2 - v_0^2) \).

Favorite