Wind Correction Angle Calculator

True Airspeed (\( \text{TAS} \)):

Course (\( \alpha \)):

Wind Speed (\( \text{WS} \)):

Wind Direction (\( \beta \)):

Wind Correction Angle (\( \theta \)):

Heading (\( \phi \)):

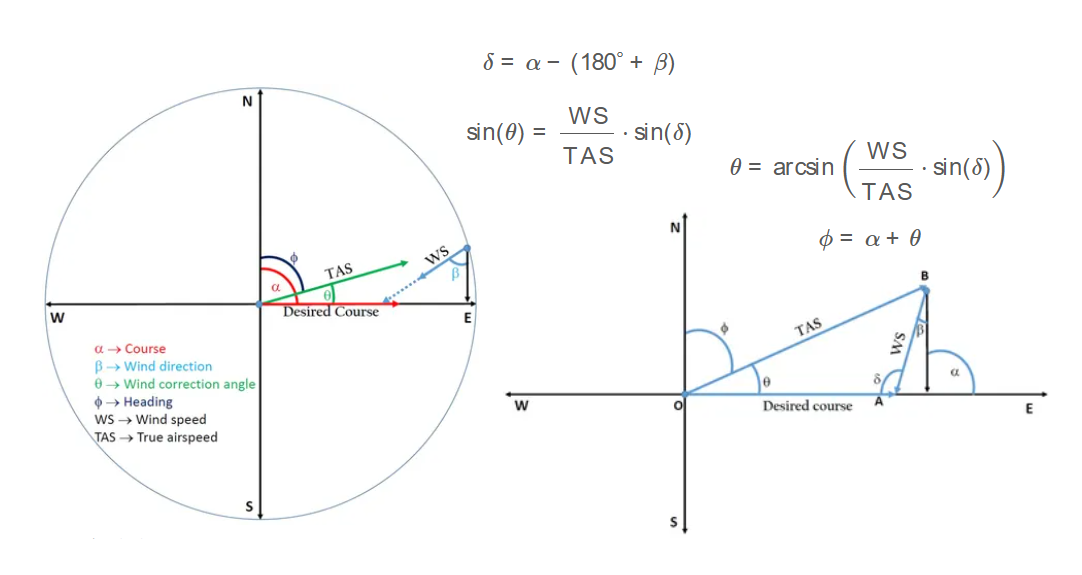
1. What is the Wind Correction Angle Calculator?

Definition: This calculator computes the wind correction angle (\( \theta \)) and the heading (\( \phi \)) of an aircraft, given the true airspeed (\( \text{TAS} \)), desired course (\( \alpha \)), wind speed (\( \text{WS} \)), and wind direction (\( \beta \)).

Purpose: It is used in aviation to adjust an aircraft's heading to compensate for wind effects, ensuring the aircraft follows the desired course.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \delta = \alpha - (180^\circ + \beta) \] \[ \sin(\theta) = \frac{\text{WS}}{\text{TAS}} \cdot \sin(\delta) \] \[ \theta = \arcsin\left(\frac{\text{WS}}{\text{TAS}} \cdot \sin(\delta)\right) \] \[ \phi = \alpha + \theta \] where:

\( \text{TAS} \): True airspeed (m/s, km/h, mph, knots, km/s, mi/s, mi/min, km/min)
\( \alpha \): Desired course (degrees or radians, clockwise from true north)
\( \text{WS} \): Wind speed (m/s, km/h, mph, knots, km/s, mi/s, mi/min, km/min)
\( \beta \): Wind direction (degrees or radians, direction from which the wind is blowing)
\( \delta \): Wind angle (degrees or radians)
\( \theta \): Wind correction angle (degrees or radians)
\( \phi \): Heading (degrees or radians, clockwise from true north)

Unit Conversions:

Speeds (\( \text{TAS} \), \( \text{WS} \)):
- 1 knot = 1 knot
- 1 m/s = 1.94384 knots
- 1 km/h = 0.539957 knots
- 1 mph = 0.868976 knots
- 1 km/s = 539.957 knots
- 1 mi/s = 868.976 knots
- 1 mi/min = 52.1386 knots
- 1 km/min = 32.3974 knots
Angles (\( \alpha \), \( \beta \), \( \delta \), \( \theta \), \( \phi \)):
- 1 degree = 1 degree
- 1 radian = \( \frac{180}{\pi} \) degrees

Steps:

Enter the true airspeed (\( \text{TAS} \)) in m/s, km/h, mph, knots, km/s, mi/s, mi/min, or km/min (default is 120 knots).
Enter the desired course (\( \alpha \)) in degrees or radians (default is 25°).
Enter the wind speed (\( \text{WS} \)) in m/s, km/h, mph, knots, km/s, mi/s, mi/min, or km/min (default is 25 knots).
Enter the wind direction (\( \beta \)) in degrees or radians (default is 150°).
Convert speeds to knots and angles to degrees for calculation.
Normalize angles to 0-360 degrees.
Calculate the wind angle (\( \delta \)) using \( \delta = \alpha - (180^\circ + \beta) \).
Calculate the wind correction angle (\( \theta \)) using the law of sines: \( \theta = \arcsin\left(\frac{\text{WS}}{\text{TAS}} \cdot \sin(\delta)\right) \).
Calculate the heading (\( \phi \)) using \( \phi = \alpha + \theta \).
Normalize the heading to 0-360 degrees if in degrees, and convert the results to the selected angle unit (degrees or radians).
Display the results, rounded to 0 decimal places for degrees or 4 decimal places for radians to match typical precision.

3. Importance of Wind Correction Angle Calculation

Calculating the wind correction angle and heading is crucial for:

Aviation Navigation: Ensuring an aircraft follows its intended course by compensating for wind drift.
Flight Planning: Adjusting flight paths to account for wind conditions, optimizing fuel efficiency and safety.
Pilot Training: Teaching pilots how to navigate in crosswind conditions effectively.

4. Using the Calculator

Examples:

Example 1: Calculate the wind correction angle and heading for an aircraft with a true airspeed of 120 knots, desired course of 25°, wind speed of 25 knots, and wind direction of 150°:
- Enter \( \text{TAS} = 120 \) knots.
- Enter \( \alpha = 25 \) degrees.
- Enter \( \text{WS} = 25 \) knots.
- Enter \( \beta = 150 \) degrees.
- Wind angle: \( \delta = 25 - (180 + 150) = 25 - 330 = -305 \), normalize to \( 360 - 305 = 55^\circ \).
- Convert \( \delta \) to radians: \( \delta = 55 \times \frac{\pi}{180} = 0.9599 \, \text{radians} \).
- Calculate \( \sin(\theta) \): \( \sin(\theta) = \frac{25}{120} \cdot \sin(0.9599) = 0.2083 \cdot 0.8192 = 0.1707 \).
- Wind correction angle: \( \theta = \arcsin(0.1707) \times \frac{180}{\pi} = 9.82^\circ \), round to \( 10^\circ \).
- Heading: \( \phi = 25 + 10 = 35^\circ \).
- Result: \( \theta = 10^\circ \), \( \phi = 35^\circ \).
Example 2: Calculate the wind correction angle and heading for an aircraft with a true airspeed of 100 m/s, desired course of 1.5708 radians, wind speed of 20 m/s, and wind direction of 4.7124 radians, with angles in radians:
- Enter \( \text{TAS} = 100 \) m/s.
- Convert to knots: \( \text{TAS} = 100 \times 1.94384 = 194.384 \, \text{knots} \).
- Enter \( \alpha = 1.5708 \) radians.
- Convert to degrees: \( \alpha = 1.5708 \times \frac{180}{\pi} = 90^\circ \).
- Enter \( \text{WS} = 20 \) m/s.
- Convert to knots: \( \text{WS} = 20 \times 1.94384 = 38.8768 \, \text{knots} \).
- Enter \( \beta = 4.7124 \) radians.
- Convert to degrees: \( \beta = 4.7124 \times \frac{180}{\pi} = 270^\circ \).
- Wind angle: \( \delta = 90 - (180 + 270) = 90 - 450 = -360 \), normalize to \( 0^\circ \).
- Convert \( \delta \) to radians: \( \delta = 0 \times \frac{\pi}{180} = 0 \, \text{radians} \).
- Calculate \( \sin(\theta) \): \( \sin(\theta) = \frac{38.8768}{194.384} \cdot \sin(0) = 0 \).
- Wind correction angle: \( \theta = \arcsin(0) = 0 \, \text{radians} \).
- Heading: \( \phi = 90 + 0 = 90^\circ \), convert to radians: \( \phi = 90 \times \frac{\pi}{180} = 1.5708 \).
- Result: \( \theta = 0.0000 \, \text{radians} \), \( \phi = 1.5708 \, \text{radians} \).

5. Frequently Asked Questions (FAQ)

Q: What is the wind correction angle?
A: The wind correction angle (\( \theta \)) is the angle an aircraft must adjust its heading by to counteract the effect of wind and maintain the desired course.

Q: Why is the wind direction given as the direction from which the wind blows?
A: In aviation, wind direction is traditionally reported as the direction from which the wind originates, measured in degrees clockwise from true north or in radians.

Q: What happens if the wind speed exceeds the true airspeed?
A: If the wind speed exceeds the true airspeed, the aircraft cannot maintain the desired course, and the calculation becomes invalid, as the wind would overpower the aircraft’s forward motion.