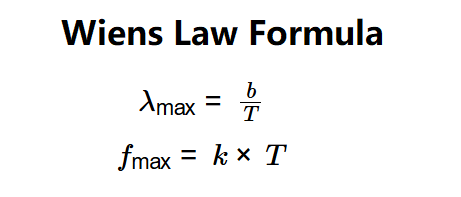Wien's Law Calculator

Peak Wavelength (\( \lambda_{\text{max}} \)):

Peak Frequency (\( f_{\text{max}} \)):

1. What is the Wien's Law Calculator?

Definition: This calculator uses Wien's displacement law to compute the peak wavelength (\( \lambda_{\text{max}} \)) and peak frequency (\( f_{\text{max}} \)) of the electromagnetic radiation emitted by a black body at a given temperature (\( T \)).

Purpose: It is used in astrophysics and thermodynamics to determine the wavelength and frequency at which a black body emits the maximum intensity of radiation, which helps in understanding the spectral characteristics of stars and other thermal emitters.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( \lambda_{\text{max}} = \frac{b}{T} \)
\( f_{\text{max}} = k \times T \)

Where:

\( \lambda_{\text{max}} \): Peak wavelength (m, cm, mm, nm, pm, Å);
\( f_{\text{max}} \): Peak frequency (Hz, kHz, MHz, GHz, THz);
\( T \): Black body temperature (K, °C, °F, converted to K);
\( b \): Wien's displacement constant (\( 2.8977719 \, \text{mm·K} \));
\( k \): Frequency constant (\( 5.8789232 \times 10^{10} \, \text{Hz/K} \)).

Steps:

Enter the black body temperature (\( T \)) with its unit.
Convert the temperature to Kelvin.
Calculate the peak wavelength: \( \lambda_{\text{max}} = \frac{b}{T} \).
Calculate the peak frequency: \( f_{\text{max}} = k \times T \).
Convert the results to the selected output units and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Wien's Law Calculation

Calculating the peak wavelength and frequency using Wien's law is crucial for:

Astrophysics: Determining the surface temperature of stars by analyzing their peak emission wavelength.
Thermodynamics: Understanding the spectral distribution of black body radiation.
Material Science: Designing thermal imaging systems and studying thermal emission properties.

4. Using the Calculator

Example 1: Calculate the peak wavelength and frequency for a black body at 300 K (room temperature):

Temperature: \( T = 300 \, \text{K} \);
Peak Wavelength: \( \lambda_{\text{max}} = \frac{2.8977719 \times 10^{-3}}{300} \approx 9.659 \times 10^{-6} \, \text{m} \approx 9659 \, \text{nm} \);
Peak Frequency: \( f_{\text{max}} = 5.8789232 \times 10^{10} \times 300 \approx 1.764 \times 10^{13} \, \text{Hz} \approx 17.64 \, \text{THz} \);
Result: \( \lambda_{\text{max}} = 9659.0000 \, \text{nm} \), \( f_{\text{max}} = 17.6400 \, \text{THz} \).

Example 2: Calculate the peak wavelength and frequency for a star at 5800 K (approximate surface temperature of the Sun):

Temperature: \( T = 5800 \, \text{K} \);
Peak Wavelength: \( \lambda_{\text{max}} = \frac{2.8977719 \times 10^{-3}}{5800} \approx 4.996 \times 10^{-7} \, \text{m} \approx 499.6 \, \text{nm} \);
Peak Frequency: \( f_{\text{max}} = 5.8789232 \times 10^{10} \times 5800 \approx 3.410 \times 10^{14} \, \text{Hz} \approx 341.0 \, \text{THz} \);
Result: \( \lambda_{\text{max}} = 499.6000 \, \text{nm} \), \( f_{\text{max}} = 341.0000 \, \text{THz} \).

5. Frequently Asked Questions (FAQ)

Q: What does Wien's law tell us?
A: Wien's law describes the relationship between the temperature of a black body and the wavelength or frequency at which it emits the maximum intensity of radiation, helping to identify the peak emission in the spectrum.

Q: Why is the peak wavelength inversely proportional to temperature?
A: As the temperature increases, the black body emits more energy, shifting the peak of the radiation to shorter wavelengths (higher frequencies), which is why \( \lambda_{\text{max}} \propto \frac{1}{T} \).

Q: Can this calculator be used for non-black bodies?
A: Wien's law strictly applies to ideal black bodies. For real objects, the peak wavelength and frequency may shift slightly due to emissivity variations, but the law provides a good approximation for near-black bodies.