Wheatstone Bridge Calculator

Calculation Type:

Resistance \( R_1 \):

Resistance \( R_2 \):

Resistance \( R_3 \):

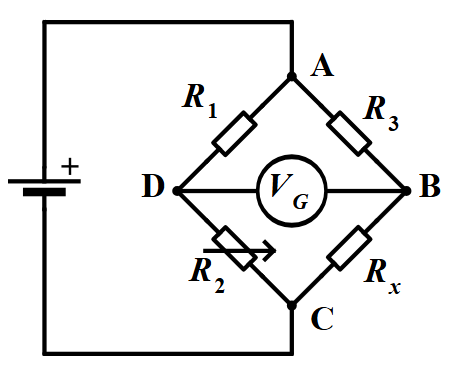
1. What is Wheatstone Bridge Calculator?

Definition: This calculator computes the unknown resistance (\( R_x \)) in a balanced Wheatstone bridge or the output voltage (\( V_G \)) across the galvanometer in an unbalanced Wheatstone bridge.

Purpose: It is used in electrical engineering to measure unknown resistances with high precision or to analyze the behavior of a Wheatstone bridge circuit under unbalanced conditions.

2. How Does the Calculator Work?

The calculator supports two types of calculations:

Balanced Wheatstone Bridge (Find Unknown Resistance):

\( \frac{R_1}{R_2} = \frac{R_3}{R_x} \)
\( R_x = \frac{R_2}{R_1} \times R_3 \)

Unbalanced Wheatstone Bridge (Find Output Voltage):

\( V_G = V \left( \frac{R_1}{R_1 + R_2} - \frac{R_3}{R_3 + R_x} \right) \)

Where:

\( R_1, R_2, R_3 \): Known resistances (Ω);
\( R_x \): Unknown resistance (Ω);
\( V \): Supply voltage across the bridge (V);
\( V_G \): Output voltage across the galvanometer (V).

Steps:

Select the calculation type (balanced or unbalanced).
Enter the required values (\( R_1 \), \( R_2 \), \( R_3 \), and for unbalanced, \( R_x \) and \( V \)) with their units.
Convert resistances to ohms and voltage to volts.
Calculate the unknown resistance (\( R_x \)) for a balanced bridge or the output voltage (\( V_G \)) for an unbalanced bridge using the appropriate formula.
Convert the output resistance or voltage to the selected output unit (Ω/kΩ for resistance, V/mV for voltage).
Display results in scientific notation if their absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Wheatstone Bridge Calculation

Calculating parameters in a Wheatstone bridge is crucial for:

Resistance Measurement: Precisely measuring unknown resistances in laboratory and industrial settings, often used in strain gauges and sensors.
Circuit Analysis: Analyzing the behavior of bridge circuits under balanced and unbalanced conditions, which is essential for designing sensitive measurement systems.
Education and Experimentation: Teaching fundamental concepts of electrical circuits and demonstrating the principles of balance in bridge circuits.

4. Using the Calculator

Example 1 (Balanced Wheatstone Bridge): Calculate the unknown resistance for a balanced Wheatstone bridge with \( R_1 = 6 \, \text{Ω} \), \( R_2 = 9 \, \text{Ω} \), and \( R_3 = 4 \, \text{Ω} \):

Input Values:
Calculation Type: Balanced;
\( R_1 = 6 \, \text{Ω} \);
\( R_2 = 9 \, \text{Ω} \);
\( R_3 = 4 \, \text{Ω} \);
Unknown Resistance: \( R_x = \frac{R_2}{R_1} \times R_3 = \frac{9}{6} \times 4 = 6 \, \text{Ω} \);
Result: \( R_x = 6.0000 \, \text{Ω} \).

Example 2 (Unbalanced Wheatstone Bridge): Calculate the output voltage for an unbalanced Wheatstone bridge with \( R_1 = 6 \, \text{Ω} \), \( R_2 = 9 \, \text{Ω} \), \( R_3 = 4 \, \text{Ω} \), \( R_x = 5 \, \text{Ω} \), and \( V = 3 \, \text{V} \):

Input Values:
Calculation Type: Unbalanced;
\( R_1 = 6 \, \text{Ω} \);
\( R_2 = 9 \, \text{Ω} \);
\( R_3 = 4 \, \text{Ω} \);
\( R_x = 5 \, \text{Ω} \);
\( V = 3 \, \text{V} \);
Output Voltage: \( V_G = V \left( \frac{R_1}{R_1 + R_2} - \frac{R_3}{R_3 + R_x} \right) = 3 \left( \frac{6}{6 + 9} - \frac{4}{4 + 5} \right) = 3 \left( \frac{6}{15} - \frac{4}{9} \right) = 3 \left( 0.4 - \frac{4}{9} \right) \approx 3 \times (0.4 - 0.4444) \approx -0.1333 \, \text{V} \);
Result: \( V_G = -1.3330e-1 \, \text{V} \).

5. Frequently Asked Questions (FAQ)

Q: What does it mean for a Wheatstone bridge to be balanced?
A: A Wheatstone bridge is balanced when the ratio of resistances satisfies \( \frac{R_1}{R_2} = \frac{R_3}{R_x} \), resulting in zero current through the galvanometer (\( V_G = 0 \)), meaning points D and B are at the same potential.

Q: Why is the output voltage zero in a balanced Wheatstone bridge?
A: In a balanced Wheatstone bridge, the voltage drops across the two arms are equal, so the potential difference between the midpoints (D and B) is zero, resulting in no current through the galvanometer and thus \( V_G = 0 \).

Q: Can this calculator be used for Wheatstone bridges with non-resistive elements?
A: This calculator assumes all elements are resistors. For bridges with capacitors, inductors, or other components, impedance-based analysis is required, which is not supported by this calculator.