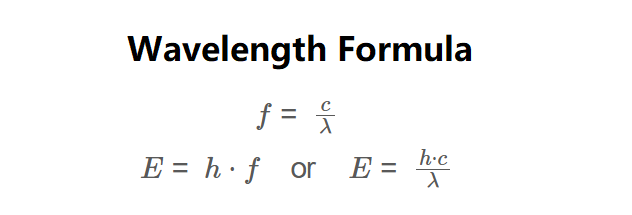Wavelength to Energy and Frequency Calculator

Energy (\( E \)):

Frequency (\( f \)):

1. What is the Wavelength to Energy Calculator?

Definition: This calculator computes the energy (\( E \)) and frequency (\( f \)) of a photon based on its wavelength (\( \lambda \)).

Purpose: It is used in physics and optics to determine the energy and frequency of photons, aiding in applications like spectroscopy and quantum mechanics.

2. How Does the Calculator Work?

The calculator uses the following formulas:

\( f = \frac{c}{\lambda} \)

\( E = h \cdot f \quad \text{or} \quad E = \frac{h \cdot c}{\lambda} \)

Where:

\( E \): Photon energy (nJ, J, neV, µeV, meV, eV, keV, MeV);
\( h \): Planck's constant (\( 6.6261 \times 10^{-34} \, \text{J·s} \) or \( 4.1357 \times 10^{-15} \, \text{eV·s} \));
\( c \): Speed of light (\( 299792458 \, \text{m/s} \));
\( \lambda \): Wavelength (m, nm, µm, mm, cm);
\( f \): Frequency (Hz, kHz, MHz, GHz, THz).

Steps:

Enter the wavelength (\( \lambda \)) with its unit.
Convert wavelength to meters.
Calculate the frequency using \( f = \frac{c}{\lambda} \).
Calculate the energy using \( E = h \cdot f \).
Convert the results to the selected output units.
Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Photon Energy and Frequency Calculation

Calculating the energy and frequency of a photon from its wavelength is crucial for:

Quantum Mechanics: Understanding photon interactions.
Optics: Analyzing light properties in spectroscopy.
Physics Education: Demonstrating Planck's relation.

4. Using the Calculator

Example 1: Calculate the energy and frequency with \( \lambda = 500 \, \text{nm} \):

Wavelength: \( \lambda = 500 \, \text{nm} \times 10^{-9} = 5 \times 10^{-7} \, \text{m} \);
Frequency: \( f = \frac{299792458}{5 \times 10^{-7}} = 5.9958 \times 10^{14} \, \text{Hz} \);
Energy: \( E = 4.1357 \times 10^{-15} \times 5.9958 \times 10^{14} \approx 2.4795 \, \text{eV} \);
Result (Energy in eV): \( E = 2.4795 \, \text{eV} \);
Result (Frequency in THz): \( f = 599.5849 \, \text{THz} \).

Example 2: Calculate the energy and frequency with \( \lambda = 1 \, \text{µm} \):

Wavelength: \( \lambda = 1 \, \text{µm} \times 10^{-6} = 1 \times 10^{-6} \, \text{m} \);
Frequency: \( f = \frac{299792458}{1 \times 10^{-6}} = 2.9979 \times 10^{14} \, \text{Hz} \);
Energy: \( E = 6.6261 \times 10^{-34} \times 2.9979 \times 10^{14} \approx 1.9866 \times 10^{-19} \, \text{J} \);
Result (Energy in nJ): \( E = 1.9866 \times 10^{-10} \, \text{nJ} \);
Result (Frequency in GHz): \( f = 299792.4580 \, \text{GHz} \).

5. Frequently Asked Questions (FAQ)

Q: What is Planck's relation?
A: Planck's relation (\( E = h \cdot f \)) states that a photon's energy is proportional to its frequency, with \( h \) as Planck's constant.

Q: Why does energy decrease with increasing wavelength?
A: Since \( E = \frac{h \cdot c}{\lambda} \), energy is inversely proportional to wavelength—longer wavelengths correspond to lower frequencies and thus lower energy.

Q: Can this calculator be used for any type of wave?
A: This calculator is designed for electromagnetic waves (photons), where the speed of light (\( c \)) applies. It does not apply to other types of waves, like sound waves.