1. What is a Time of Flight Calculator?

Definition: This calculator determines the time of flight for a projectile launched at an angle from a certain height, accounting for gravity.

Purpose: It is used in physics to calculate how long a projectile remains in the air, aiding in trajectory planning and analysis.

2. How Does the Calculator Work?

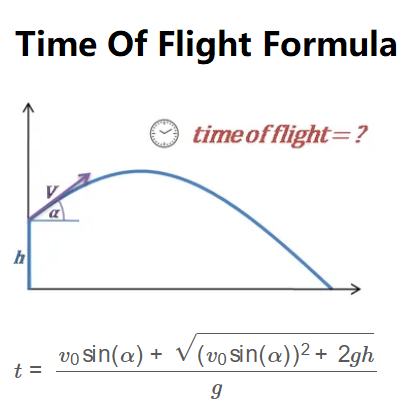
The calculator uses the following formula:

\[ t = \frac{v_0 \sin(\alpha) + \sqrt{(v_0 \sin(\alpha))^2 + 2gh}}{g} \] Where:

• \(t\): Time of flight (s, min, hour)
• \(v_0\): Initial velocity (m/s, km/h)
• \(\alpha\): Launch angle (degrees, radians)
• \(h\): Initial height (m, km)
• \(g\): Gravitational acceleration (m/s², g)

Unit Conversions:

• Velocity (v₀): m/s, km/h (1 km/h = 0.277778 m/s)
• Angle (α): degrees, radians (1 degree = π/180 radians)
• Height (h): m, km (1 km = 1000 m)
• Gravity (g): m/s², g (1 g = 9.81 m/s²)
• Time (t): s, min, hour (1 min = 60 s, 1 hour = 3600 s)

Steps:

• Enter the initial velocity (v₀), selecting the unit (m/s, km/h).
• Enter the launch angle (α), selecting the unit (degrees, radians).
• Enter the initial height (h), selecting the unit (m, km).
• Enter the gravitational acceleration (g), selecting the unit (m/s², g).
• Convert all inputs to base units (m/s, radians, m, m/s²).
• Calculate the time of flight using the formula.
• Convert the result to the selected time unit and display.

3. Importance of Time of Flight Calculation

Calculating the time of flight is crucial for:

• Trajectory Planning: Determining how long a projectile will stay in the air.
• Sports: Analyzing the flight of a ball in sports like baseball or golf.
• Engineering: Designing projectiles or launch systems.

4. Using the Calculator

Examples:

• Example 1: For \(v_0 = 20 \, \text{m/s}\), \(\alpha = 45^\circ\), \(h = 10 \, \text{m}\), \(g = 9.81 \, \text{m/s²}\):
  • Convert: \(\alpha = \frac{\pi}{4} \, \text{radians}\), \(\sin(\alpha) = \frac{\sqrt{2}}{2}\)
  • \(v_0 \sin(\alpha) = 20 \times \frac{\sqrt{2}}{2} = 14.142 \, \text{m/s}\)
  • Discriminant: \((v_0 \sin(\alpha))^2 + 2gh = 14.142^2 + 2 \times 9.81 \times 10 = 200 + 196.2 = 396.2\)
  • Time: \(t = \frac{14.142 + \sqrt{396.2}}{9.81} = \frac{14.142 + 19.905}{9.81} = 3.472 \, \text{s}\)
• Example 2: For \(v_0 = 36 \, \text{km/h}\), \(\alpha = \frac{\pi}{3} \, \text{radians}\), \(h = 0.1 \, \text{km}\), \(g = 1 \, \text{g}\):
  • Convert: \(v_0 = 10 \, \text{m/s}\), \(h = 100 \, \text{m}\), \(g = 9.81 \, \text{m/s²}\)
  • \(\sin(\alpha) = \sin(\frac{\pi}{3}) = \frac{\sqrt{3}}{2}\)
  • \(v_0 \sin(\alpha) = 10 \times \frac{\sqrt{3}}{2} = 8.66 \, \text{m/s}\)
  • Discriminant: \((8.66)^2 + 2 \times 9.81 \times 100 = 75 + 1962 = 2037\)
  • Time: \(t = \frac{8.66 + \sqrt{2037}}{9.81} = \frac{8.66 + 45.13}{9.81} = 5.484 \, \text{s}\)

5. Frequently Asked Questions (FAQ)

Q: What if the initial height is zero?
A: The formula still works; the term \(2gh\) becomes zero, simplifying the calculation.

Q: What if the discriminant is negative?
A: A negative discriminant means no real solution exists, likely due to invalid inputs.

Q: Can I use this for vertical launches?
A: Yes, set \(\alpha = 90^\circ\), and the formula will compute the time to reach the ground.

Time of Flight Calculator© - All Rights Reserved 2025