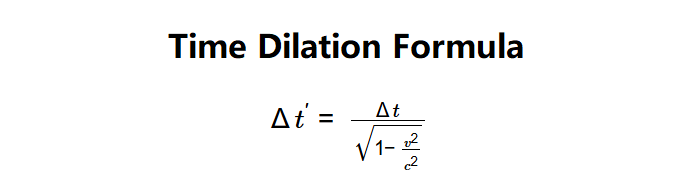Time Dilation Calculator

Observer's Time (\( \Delta t \)):

Relative Velocity (\( v \)):

1. What is Time Dilation Calculator?

Definition: This calculator computes the time dilation effect predicted by Einstein's special relativity, showing how time passes differently for a moving observer compared to a stationary one.

Purpose: It is used to understand how time slows down for an object moving at high speeds relative to a stationary observer, applicable in scenarios like space travel or high-speed particle physics.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( \Delta t' = \frac{\Delta t}{\sqrt{1 - \frac{v^2}{c^2}}} \)

Where:

\( \Delta t' \): Time elapsed in the moving frame (traveler's time)
\( \Delta t \): Time elapsed in the stationary frame (observer's time, e.g., on Earth)
\( v \): Relative velocity of the moving frame
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))

Steps:

Enter the observer's time (\( \Delta t \)) with its respective unit (sec, min, hr, days, wk, mos, yrs).
Enter the relative velocity (\( v \)) with its respective unit (m/s, km/h, ft/s, mph, km/s, mi/s, c).
Convert the time to seconds and the velocity to meters per second.
Calculate the traveler's time using the time dilation formula.
Convert the result to the selected output time unit.
Display the result with 4 decimal places.

3. Importance of Time Dilation Calculation

Calculating time dilation is crucial for:

Space Travel: Understanding how time passes for astronauts traveling at high speeds, e.g., during interstellar missions.
Particle Physics: Explaining why fast-moving particles, like muons, decay more slowly than expected.
Education: Illustrating a key concept of Einstein’s special relativity.

4. Using the Calculator

Example: An observer on Earth measures 10 years, and a spaceship travels at 0.9c:

Observer's Time (\( \Delta t \)): 10 years = \( 10 \times 365.25 \times 24 \times 3600 = 315,576,000 \) seconds
Velocity (\( v \)): \( 0.9c = 0.9 \times 299,792,458 = 269,813,212.2 \) m/s
Lorentz Factor (\( \gamma \)): \( \frac{1}{\sqrt{1 - (0.9)^2}} = \frac{1}{\sqrt{0.19}} \approx 2.294 \)
Traveler's Time (\( \Delta t' \)): \( \frac{315,576,000}{2.294} \approx 137,565,389 \) seconds
Convert to years: \( 137,565,389 / (365.25 \times 24 \times 3600) \approx 4.36 \) years
Result: \( \Delta t' = 4.3600 \) years

5. Frequently Asked Questions (FAQ)

Q: What is time dilation?
A: Time dilation is a prediction of special relativity where time passes slower for a moving object relative to a stationary observer, as described by the formula \( \Delta t' = \frac{\Delta t}{\sqrt{1 - \frac{v^2}{c^2}}} \).

Q: Why does time slow down at high speeds?
A: As an object approaches the speed of light, the Lorentz factor (\( \gamma \)) increases, causing the denominator in the formula to shrink, thus increasing the traveler’s perceived time relative to the observer’s time.

Q: Can velocity exceed the speed of light?
A: No, according to special relativity, no object with mass can reach or exceed the speed of light (\( c \)). The calculator will display an error if \( v \geq c \).