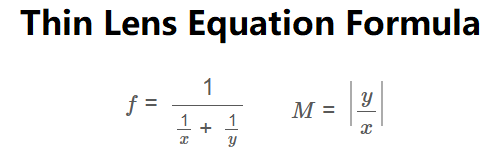Thin Lens Equation Calculator

Object Distance (\( x \)):

Image Distance (\( y \)):

1. What is Thin Lens Equation Calculator?

Definition: This calculator computes the focal length (\( f \)) and magnification (\( M \)) of a thin lens based on the object distance (\( x \)) and image distance (\( y \)), using the thin lens equation.

Purpose: It is used in optics to determine the focal length of a lens and the magnification of the image formed, aiding in lens design and understanding image formation.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Thin Lens Equation: \[ \frac{1}{x} + \frac{1}{y} = \frac{1}{f} \] Rearranged to solve for \( f \): \[ f = \frac{1}{\frac{1}{x} + \frac{1}{y}} \] Magnification: \[ M = \left| \frac{y}{x} \right| \] Where:

\( x \): Object distance (mm, cm, m, km, in, ft, yd, mi)
\( y \): Image distance (mm, cm, m, km, in, ft, yd, mi)
\( f \): Focal length (mm, cm, m, km, in, ft, yd, mi)
\( M \): Magnification (dimensionless)

Unit Conversions:

Distance (\( x \), \( y \), \( f \)): mm, cm (1 cm = 10 mm), m (1 m = 1000 mm), km (1 km = 1000000 mm), in (1 in = 25.4 mm), ft (1 ft = 304.8 mm), yd (1 yd = 914.4 mm), mi (1 mi = 1609344 mm)

Steps:

Enter the object distance (\( x \)) and image distance (\( y \)), and select their units.
Convert \( x \) and \( y \) to mm for calculation.
Validate inputs: \( x \) and \( y \) cannot be zero.
Calculate the focal length: \( f = \frac{1}{\frac{1}{x} + \frac{1}{y}} \).
Calculate the magnification: \( M = \left| \frac{y}{x} \right| \).
Convert the focal length to the selected focal length unit.
Display the results, using scientific notation for focal length values less than 0.001, otherwise with 4 decimal places.

3. Importance of Thin Lens Equation Calculation

Calculating the focal length and magnification using the thin lens equation is crucial for:

Optical Design: Designing lenses for cameras, microscopes, and telescopes by determining their focal lengths.
Physics Education: Understanding the principles of image formation by lenses.
Photography: Adjusting lens parameters to achieve desired image sizes and positions.

4. Using the Calculator

Examples:

Example 1: For \( x = 100 \, \text{mm} \), \( y = 200 \, \text{mm} \), focal length in mm:
- Focal Length: \( \frac{1}{f} = \frac{1}{100} + \frac{1}{200} = 0.015 \), \( f = \frac{1}{0.015} \approx 66.6667 \, \text{mm} \)
- Magnification: \( M = \left| \frac{200}{100} \right| = 2.0000 \)
Example 2: For \( x = 50 \, \text{cm} \), \( y = -100 \, \text{cm} \), focal length in cm:
- Convert: \( x = 50 \times 10 = 500 \, \text{mm} \), \( y = -100 \times 10 = -1000 \, \text{mm} \)
- Focal Length: \( \frac{1}{f} = \frac{1}{500} + \frac{1}{-1000} = 0.001 \), \( f = \frac{1}{0.001} = 1000 \, \text{mm} = 100 \, \text{cm} \)
- Magnification: \( M = \left| \frac{-1000}{500} \right| = 2.0000 \)
Example 3: For \( x = 1 \, \text{m} \), \( y = 2 \, \text{m} \), focal length in km:
- Convert: \( x = 1 \times 1000 = 1000 \, \text{mm} \), \( y = 2 \times 1000 = 2000 \, \text{mm} \)
- Focal Length: \( \frac{1}{f} = \frac{1}{1000} + \frac{1}{2000} = 0.0015 \), \( f = \frac{1}{0.0015} \approx 666.6667 \, \text{mm} \approx 0.0007 \, \text{km} \)
- Magnification: \( M = \left| \frac{2000}{1000} \right| = 2.0000 \)

5. Frequently Asked Questions (FAQ)

Q: What is the thin lens equation?
A: The thin lens equation relates the object distance (\( x \)), image distance (\( y \)), and focal length (\( f \)) of a lens, allowing the prediction of image position.

Q: What does a negative image distance mean?
A: A negative image distance (\( y \)) indicates a virtual image formed on the same side of the lens as the object, typically for diverging lenses or when the object is inside the focal point of a converging lens.

Q: Why must the magnification be positive?
A: Magnification is defined as the absolute value of the ratio \( \frac{y}{x} \) to represent the size ratio of the image to the object, regardless of orientation (upright or inverted).