1. What is the Thermodynamic Processes Calculator (Isobaric)?

Definition: This calculator computes key thermodynamic properties for an isobaric process (constant pressure) involving an ideal gas. It calculates the final volume (\( V_2 \)), number of moles (\( n \)), internal energy change (\( \Delta U \)), work done (\( W \)), and heat absorbed (\( Q \)).

Purpose: It is used in thermodynamics to analyze processes where a gas expands or contracts at constant pressure, such as in piston-cylinder systems, heat engines, or atmospheric processes.

2. How Does the Calculator Work?

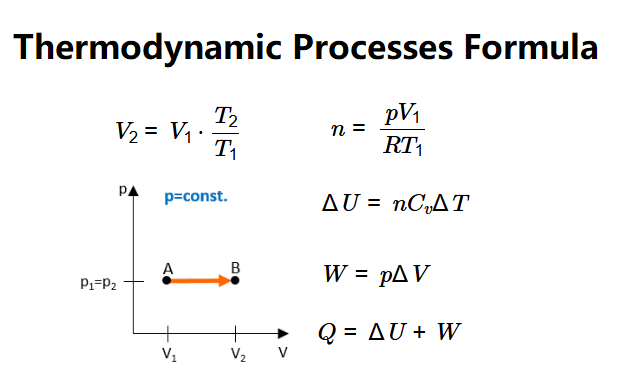
The calculator uses the following equations for an isobaric process:

Formulas:

• Final Volume: \[ V_2 = V_1 \cdot \frac{T_2}{T_1} \]
• Number of Moles: \[ n = \frac{p V_1}{R T_1} \]
• Internal Energy Change: \[ \Delta U = n C_v \Delta T \]
• Work Done: \[ W = p \Delta V \]
• Heat Absorbed: \[ Q = \Delta U + W \]

where:

• \( V_1, V_2 \): Initial and final volumes in mm³, cm³, m³, L, mL, ft³
• \( T_1, T_2 \): Initial and final temperatures in K, °C, °F
• \( p \): Pressure in Pa, kPa, atm
• \( R \): Gas constant, 8.314 J/(mol·K)
• \( n \): Number of moles in mol
• \( C_v \): Heat capacity at constant volume in J/(mol·K)
• \( \Delta T = T_2 - T_1 \): Temperature change
• \( \Delta V = V_2 - V_1 \): Volume change
• \( \Delta U, W, Q \): Internal energy change, work done, and heat absorbed in J, kJ, MJ, Wh, kWh, ft-lb, kcal

Unit Conversions:

• Volume (\( V_1, V_2 \)):
  • 1 mm³ = \( 1 \times 10^{-9} \, \text{m}^3 \)
  • 1 cm³ = \( 1 \times 10^{-6} \, \text{m}^3 \)
  • 1 m³ = 1 m³
  • 1 L = 0.001 m³
  • 1 mL = \( 1 \times 10^{-6} \, \text{m}^3 \)
  • 1 ft³ = 0.0283168 m³
• Temperature (\( T_1, T_2 \)):
  • Kelvin (K): No conversion needed
  • Celsius (°C) to Kelvin: \( T_K = T_C + 273.15 \)
  • Fahrenheit (°F) to Kelvin: \( T_K = (T_F - 32) \cdot \frac{5}{9} + 273.15 \)
• Pressure (\( p \)):
  • 1 Pa = 1 Pa
  • 1 kPa = 1000 Pa
  • 1 atm = 101325 Pa
• Energy (\( \Delta U, W, Q \)):
  • 1 J = 1 J
  • 1 kJ = 1000 J
  • 1 MJ = \( 1 \times 10^6 \, \text{J} \)
  • 1 Wh = 3600 J
  • 1 kWh = \( 3.6 \times 10^6 \, \text{J} \)
  • 1 ft-lb = \( \frac{1}{0.737562} \approx 1.35582 \, \text{J} \)
  • 1 kcal = 4184 J

Steps:

• Enter the initial volume (\( V_1 \)) in mm³, cm³, m³, L, mL, or ft³.
• Enter the initial temperature (\( T_1 \)) and final temperature (\( T_2 \)) in K, °C, or °F.
• Enter the pressure (\( p \)) in Pa, kPa, or atm.
• Select a gas to use its predefined heat capacity (\( C_v \)) or choose "Custom" to enter a custom value in J/(mol·K).
• Convert all inputs to SI units (m³ for volume, Kelvin for temperature, Pa for pressure).
• Calculate \( V_2 \), \( n \), \( \Delta U \), \( W \), and \( Q \) using the formulas above.
• Convert the results to the selected units (defaulting to kJ for energy outputs) and display them, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Thermodynamic Processes Calculation

Calculating properties of thermodynamic processes is crucial for:

• Engineering Systems: It helps in designing engines, refrigerators, and HVAC systems where gases undergo expansion or compression.
• Energy Analysis: Understanding heat and work interactions aids in optimizing energy efficiency in industrial processes.
• Scientific Research: It provides insights into the behavior of gases under various conditions, essential for developing new technologies.

4. Using the Calculator

Examples:

• Example 1: Calculate the thermodynamic properties of nitrogen gas in a flexible container with an initial volume of 0.5 m³ at 77 °F and atmospheric pressure (101.325 kPa), heated to 80.33 °F:
  • Enter Initial Volume = 0.5 m³.
  • Enter Initial Temperature = 77 °F, convert to K: \( (77 - 32) \times \frac{5}{9} + 273.15 = 298.15 \, \text{K} \).
  • Enter Final Temperature = 80.33 °F, convert to K: \( (80.33 - 32) \times \frac{5}{9} + 273.15 = 300 \, \text{K} \).
  • Enter Pressure = 101.325 kPa, convert to Pa: \( 101.325 \times 1000 = 101325 \, \text{Pa} \).
  • Select Gas: Nitrogen (\( C_v = 20.814 \, \text{J/(mol·K)} \)).
  • Final Volume: \( V_2 = V_1 \cdot \frac{T_2}{T_1} = 0.5 \times \frac{300}{298.15} = 0.5031 \, \text{m}^3 \).
  • Number of Moles: \( n = \frac{p V_1}{R T_1} = \frac{101325 \times 0.5}{8.314 \times 298.15} = 20.465 \, \text{mol} \).
  • Internal Energy Change: \( \Delta U = n C_v \Delta T = 20.465 \times 20.814 \times (300 - 298.15) = 787.7 \, \text{J} = 0.7877 \, \text{kJ} \).
  • Work Done: \( W = p \Delta V = 101325 \times (0.5031 - 0.5) = 314.1 \, \text{J} = 0.3141 \, \text{kJ} \).
  • Heat Absorbed: \( Q = \Delta U + W = 787.7 + 314.1 = 1101.8 \, \text{J} = 1.1018 \, \text{kJ} \).
  • Results: \( V_2 = 0.5031 \, \text{m}^3 \), \( n = 20.4650 \, \text{mol} \), \( \Delta U = 0.7877 \, \text{kJ} \), \( W = 0.3141 \, \text{kJ} \), \( Q = 1.1018 \, \text{kJ} \).

5. Frequently Asked Questions (FAQ)

Q: What is an isobaric process?
A: An isobaric process is a thermodynamic process where the pressure remains constant while the volume and temperature of the gas change.

Q: Why is \( C_v \) used for internal energy change in an isobaric process?
A: For an ideal gas, the internal energy (\( U \)) depends only on temperature, and \( \Delta U = n C_v \Delta T \), regardless of the process. \( C_v \) is the heat capacity at constant volume, reflecting the energy change due to temperature.

Q: What are some real-world applications of isobaric processes?
A: Isobaric processes occur in piston-cylinder systems (e.g., in car engines), atmospheric processes (e.g., air heating in weather systems), and certain stages of thermodynamic cycles (e.g., Rankine cycle in power plants).

Thermodynamic Processes Calculator© - All Rights Reserved 2025