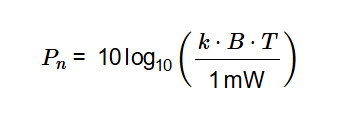1. What is Noise Power?
Definition: Noise power (\( P_n \)) is the power generated by thermal noise in a system, often referred to as Johnson-Nyquist noise. It is a fundamental limit in RF systems and is measured in dBm.
Purpose: This calculator determines the noise power in a given bandwidth at a specified temperature, which is critical for assessing the noise floor in RF receivers and communication systems.
2. How Does the Calculator Work?
The calculator uses the following formula for noise power:
Noise Power (\( P_n \)):
\[
P_n = 10 \log_{10} \left( \frac{k \cdot B \cdot T}{1 \, \text{mW}} \right)
\]
Where:
- \( P_n \): Noise power (in dBm)
- \( k \): Boltzmann’s constant (\( 1.38064852 \times 10^{-23} \, \text{J/K} \))
- \( B \): Bandwidth (converted to Hz from Hz, kHz, MHz, or GHz)
- \( T \): Temperature (converted to Kelvin from K or °C)
- 1 mW: Reference power for dBm conversion (\( 0.001 \, \text{W} \))
Steps:
- Enter the bandwidth \( B \) and select its unit (Hz, kHz, MHz, GHz).
- Enter the temperature \( T \) and select its unit (Kelvin or Celsius).
- Click "Calculate" to compute the noise power.
- The result is displayed in dBm with 4 decimal places, or in scientific notation if less than 0.001.
3. Importance of Noise Power Calculations
Noise power calculations are essential for:
- Receiver Sensitivity: Determines the noise floor, which affects the minimum detectable signal in RF receivers.
- System Design: Helps engineers design systems with adequate signal-to-noise ratios for reliable communication.
- Performance Analysis: Evaluates the impact of thermal noise on the overall performance of RF systems.
4. Using the Calculator
Examples:
- Example 1: Room Temperature at 1 MHz Bandwidth
- \( B = 1 \, \text{MHz} = 1 \times 10^6 \, \text{Hz} \), \( T = 290 \, \text{K} \)
- \( P_n = 10 \log_{10} \left( \frac{1.38064852 \times 10^{-23} \times 1 \times 10^6 \times 290}{0.001} \right) \approx -113.9770 \, \text{dBm} \)
- Example 2: High Bandwidth at 25°C
- \( B = 10 \, \text{GHz} = 10 \times 10^9 \, \text{Hz} \), \( T = 25 \, ^\circ\text{C} = 298.15 \, \text{K} \)
- \( P_n = 10 \log_{10} \left( \frac{1.38064852 \times 10^{-23} \times 10 \times 10^9 \times 298.15}{0.001} \right) \approx -83.7557 \, \text{dBm} \)
- Example 3: Low Temperature at 100 kHz
- \( B = 100 \, \text{kHz} = 100 \times 10^3 \, \text{Hz} \), \( T = 77 \, \text{K} \ (liquid nitrogen temperature) \)
- \( P_n = 10 \log_{10} \left( \frac{1.38064852 \times 10^{-23} \times 100 \times 10^3 \times 77}{0.001} \right) \approx -126.7148 \, \text{dBm} \)
5. Frequently Asked Questions (FAQ)
Q: What is thermal noise?
A: Thermal noise, also known as Johnson-Nyquist noise, is the random noise generated by the thermal agitation of electrons in a conductor, proportional to temperature and bandwidth.
Q: Why is noise power expressed in dBm?
A: dBm is a logarithmic unit that expresses power relative to 1 milliwatt (mW), commonly used in RF engineering to represent small noise power levels conveniently.
Q: How does temperature affect noise power?
A: Noise power is directly proportional to temperature (\( P_n \propto T \)). Higher temperatures increase thermal agitation, resulting in higher noise power.
 Home
Home
 Back
Back