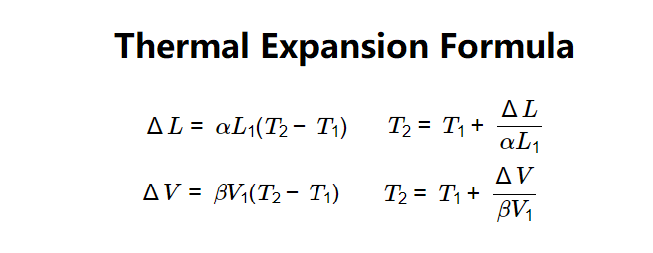Thermal Expansion Calculator

Calculate:

Initial Temperature (\( T_1 \)):

Initial Length (\( L_1 \)):

Linear Expansion Coefficient (\( \alpha \)):

Final Temperature (\( T_2 \)):

1. What is the Thermal Expansion Calculator?

Definition: This calculator computes the change in length (\( \Delta L \)) or volume (\( \Delta V \)) of an object due to temperature changes, using the principles of linear and volumetric thermal expansion. It can also calculate the final temperature (\( T_2 \)) if the change in length or volume is known.

Purpose: It is used in physics and engineering to predict how materials expand or contract with temperature changes, which is critical in designing structures, machinery, and systems like bridges, railways, and pipelines.

2. How Does the Calculator Work?

The calculator uses the following thermal expansion formulas:

Formulas:

Linear Expansion: \[ \Delta L = \alpha L_1 (T_2 - T_1) \] To find the final temperature: \[ T_2 = T_1 + \frac{\Delta L}{\alpha L_1} \]
Volumetric Expansion: \[ \Delta V = \beta V_1 (T_2 - T_1) \] To find the final temperature: \[ T_2 = T_1 + \frac{\Delta V}{\beta V_1} \]

where:

\( \Delta L \): Change in length (mm, cm, m, in, ft)
\( L_1 \): Initial length (mm, cm, m, in, ft)
\( \alpha \): Linear expansion coefficient (per K, per °C, per °F)
\( \Delta V \): Change in volume (mm³, cm³, m³, L, mL, ft³)
\( V_1 \): Initial volume (mm³, cm³, m³, L, mL, ft³)
\( \beta \): Volumetric expansion coefficient (per K, per °C, per °F)
\( T_1 \): Initial temperature (K, °C, °F)
\( T_2 \): Final temperature (K, °C, °F)

Unit Conversions:

Length (\( L_1 \), \( \Delta L \)):
- 1 mm = 0.001 m
- 1 cm = 0.01 m
- 1 m = 1 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
Volume (\( V_1 \), \( \Delta V \)):
- 1 mm³ = \( 1 \times 10^{-9} \, \text{m}^3 \)
- 1 cm³ = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 m³ = 1 m³
- 1 L = 0.001 m³
- 1 mL = \( 1 \times 10^{-6} \, \text{m}^3 \)
- 1 ft³ = 0.0283168 m³
Temperature (\( T_1 \), \( T_2 \)):
- Kelvin (K): No conversion needed
- Celsius (°C) to Kelvin: \( T_K = T_C + 273.15 \)
- Fahrenheit (°F) to Kelvin: \( T_K = (T_F - 32) \cdot \frac{5}{9} + 273.15 \)
Expansion Coefficients (\( \alpha \), \( \beta \)):
- Per K: No conversion needed
- Per °C: Same as per K for ΔT calculations
- Per °F to per K: Multiply by \( \frac{5}{9} \)

Steps:

Select whether to calculate \( \Delta L \), \( \Delta V \), or \( T_2 \) for linear or volumetric expansion.
Enter the initial temperature (\( T_1 \)) in K, °C, or °F (step size 0.01).
For linear expansion: Enter the initial length (\( L_1 \)) in mm, cm, m, in, or ft (step size 0.00001), and the linear expansion coefficient (\( \alpha \)) (step size 0.0000001) in per K, per °C, or per °F.
For volumetric expansion: Enter the initial volume (\( V_1 \)) in mm³, cm³, m³, L, mL, or ft³ (step size 0.00001), and the volumetric expansion coefficient (\( \beta \)) (step size 0.0000001) in per K, per °C, or per °F.
If calculating \( \Delta L \) or \( \Delta V \), enter the final temperature (\( T_2 \)) in K, °C, or °F (step size 0.01).
If calculating \( T_2 \), enter the change in length (\( \Delta L \)) or change in volume (\( \Delta V \)) in the selected unit.
Convert all inputs to SI units (meters for length, m³ for volume, Kelvin for temperature, expansion coefficients to per K).
Calculate the result using the appropriate formula.
Convert the result back to the selected unit and display it, using scientific notation if the absolute value is less than 0.001, otherwise rounded to 4 decimal places.

3. Importance of Thermal Expansion Calculation

Calculating thermal expansion is crucial for:

Engineering Design: It helps in designing structures like bridges, railways, and pipelines, where temperature changes can cause expansion or contraction, potentially leading to structural failure if not accounted for.
Material Selection: Understanding how materials expand helps engineers choose appropriate materials for specific temperature ranges, such as in engines or electronic devices.
Scientific Research: It aids in studying the thermal properties of materials under varying conditions, essential for developing new materials and technologies.

4. Using the Calculator

Examples:

Example 1 (Linear Expansion - ΔL): Calculate the change in length of a steel rod with an initial length of 1 m at 20 °C when heated to 100 °C (\( \alpha = 12 \times 10^{-6} \, \text{per K} \)):
- Enter Initial Length = 1 m.
- Enter Initial Temperature = 20 °C, convert to K: \( 20 + 273.15 = 293.15 \, \text{K} \).
- Enter Final Temperature = 100 °C, convert to K: \( 100 + 273.15 = 373.15 \, \text{K} \).
- Enter \( \alpha = 0.000012 \, \text{per K} \).
- Change in Length: \( \Delta L = \alpha L_1 (T_2 - T_1) = 0.000012 \times 1 \times (373.15 - 293.15) = 0.00096 \, \text{m} \).
- Convert to ft: \( 0.00096 \div 0.3048 = 0.0031496 \).
- Result: \( \Delta L = 0.0031 \, \text{ft} \).
Example 2 (Volumetric Expansion - ΔV): Calculate the change in volume of water with an initial volume of 1 ft³ at 68 °F when heated to 212 °F (\( \beta = 115 \times 10^{-6} \, \text{per °F} \)):
- Enter Initial Volume = 1 ft³, convert to m³: \( 1 \times 0.0283168 = 0.0283168 \, \text{m}^3 \).
- Enter Initial Temperature = 68 °F, convert to K: \( (68 - 32) \times \frac{5}{9} + 273.15 = 293.15 \, \text{K} \).
- Enter Final Temperature = 212 °F, convert to K: \( (212 - 32) \times \frac{5}{9} + 273.15 = 373.15 \, \text{K} \).
- Enter \( \beta = 0.000115 \, \text{per °F} \), convert to per K: \( 0.000115 \times \frac{5}{9} = 0.00006389 \, \text{per K} \).
- Change in Volume: \( \Delta V = \beta V_1 (T_2 - T_1) = 0.00006389 \times 0.0283168 \times (373.15 - 293.15) = 0.0001448 \, \text{m}^3 \).
- Convert to ft³: \( 0.0001448 \div 0.0283168 = 0.005115 \).
- Result: \( \Delta V = 0.0051 \, \text{ft}^3 \).

5. Frequently Asked Questions (FAQ)

Q: What is thermal expansion?
A: Thermal expansion is the tendency of a material to change its shape, area, or volume in response to a change in temperature. Linear expansion refers to the change in length, while volumetric expansion refers to the change in volume.

Q: Why are expansion coefficients important?
A: Expansion coefficients (\( \alpha \) and \( \beta \)) quantify how much a material expands per degree of temperature change, allowing engineers to predict and accommodate dimensional changes in materials.

Q: What are some real-world applications of thermal expansion?
A: Thermal expansion is critical in designing railway tracks (gaps prevent buckling in heat), bridges (expansion joints), and even household items like thermometers (mercury or alcohol expands with heat).