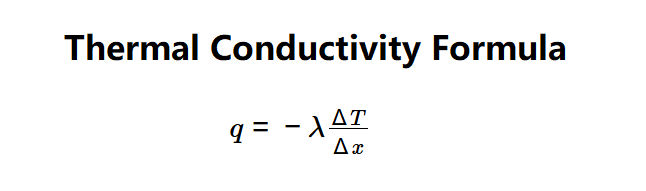Thermal Conductivity Calculator

Calculate:

Heat Flux (\( q \)):

Thermal Conductivity (\( \lambda \)):

Temperature Difference (\( \Delta T \)):

Distance (\( \Delta x \)):

1. What is Thermal Conductivity Calculator?

Definition: This calculator uses Fourier's Law to compute the heat flux (\( q \)), thermal conductivity (\( \lambda \)), temperature difference (\( \Delta T \)), or distance (\( \Delta x \)) for heat transfer through a material.

Purpose: It is used in physics, engineering, and materials science to analyze heat transfer rates, design thermal insulation, and optimize heat conduction in systems like electronics, buildings, and industrial equipment.

2. How Does the Calculator Work?

The calculator uses Fourier's Law:

\( q = -\lambda \frac{\Delta T}{\Delta x} \)

Where:

\( \lambda \): Thermal conductivity (W/(m·K));
\( \Delta T \): Temperature difference (K);
\( \Delta x \): Distance of heat transfer (m);
\( q \): Heat flux (W/m²).

Steps:

Select what to calculate: heat flux (\( q \)), thermal conductivity (\( \lambda \)), temperature difference (\( \Delta T \)), or distance (\( \Delta x \)).
Enter the known values with their respective units.
Convert all inputs to base units (W/m² for heat flux, W/(m·K) for thermal conductivity, K for temperature difference, m for distance).
Calculate the desired value using the rearranged form of Fourier's Law.
Convert the result to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Thermal Conductivity Calculation

Calculating heat flux or related parameters is crucial for:

Thermal Design: Optimizing insulation materials and heat sinks in electronics, buildings, and industrial systems.
Energy Efficiency: Reducing heat loss or gain in HVAC systems, pipelines, and thermal storage.
Material Selection: Choosing materials with appropriate thermal conductivity for specific applications, such as conductors or insulators.

4. Using the Calculator

Example 1 (Calculating Heat Flux): Calculate the heat flux through a material:

Calculate: Heat Flux (\( q \));
Thermal Conductivity: \( \lambda = 1 \, \text{W/(m·K)} \);
Temperature Difference: \( \Delta T = 10 \, \text{K} \);
Distance: \( \Delta x = 0.1 \, \text{m} \);
Heat Flux: \( q = -1 \times \frac{10}{0.1} = -100 \, \text{W/m²} \);
Result: \( q = -100.0000 \, \text{W/m²} \).

Example 2 (Calculating Thermal Conductivity): Calculate the thermal conductivity of a material:

Calculate: Thermal Conductivity (\( \lambda \));
Heat Flux: \( q = -100 \, \text{W/m²} \);
Temperature Difference: \( \Delta T = 10 \, \text{K} \);
Distance: \( \Delta x = 0.1 \, \text{m} \);
Thermal Conductivity: \( \lambda = -(-100) \times \frac{0.1}{10} = 1 \, \text{W/(m·K)} \);
Result: \( \lambda = 1.0000 \, \text{W/(m·K)} \).

5. Frequently Asked Questions (FAQ)

Q: What is heat flux?
A: Heat flux (\( q \)) is the rate of heat energy transfer per unit area, measured in W/m², and indicates how much heat flows through a surface per second.

Q: What does the negative sign in Fourier's Law mean?
A: The negative sign indicates that heat flows from a warmer to a colder region, opposite to the direction of the temperature gradient (\( \Delta T / \Delta x \)).

Q: Why can I calculate different variables?
A: Fourier's Law can be rearranged to solve for any variable (\( q \), \( \lambda \), \( \Delta T \), or \( \Delta x \)), making the calculator versatile for various heat transfer problems.