Telescope Magnification Calculator

Objective's Diameter (\( D_o \)):

f-ratio (\( f_r \)):

Eyepiece Focal Length (\( f_e \)):

Apparent Field of View (\( FOV_e \)) (degrees):

(\( FOV_e \)): typically varies from 50° to 60°

Magnification (\( M \)):

Resolving Power (\( P_r \)) (arcseconds):

True Field of View (\( FOV_s \)) (degrees):

Exit Pupil Diameter (\( D_{ep} \)) (mm):

Surface Brightness (\( SB \)) (%):

Star Magnitude Limit (\( L_m \)) (magnitude):

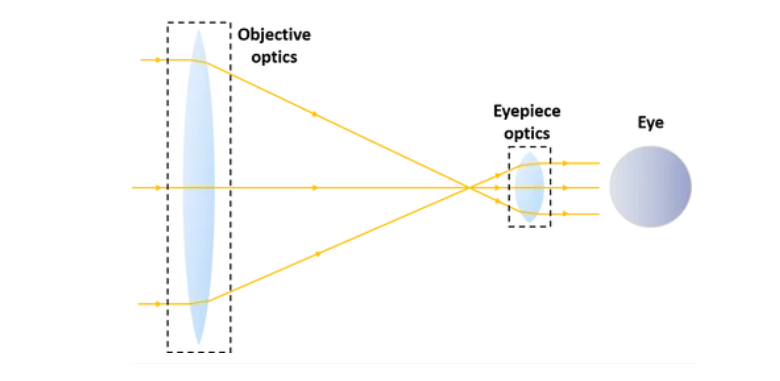
1. What is Telescope Magnification Calculator?

Definition: This calculator computes the magnification (\( M \)) and other optical parameters of a telescope based on the objective's diameter (\( D_o \)), f-ratio (\( f_r \)), and eyepiece focal length (\( f_e \)).

Purpose: It is used in astronomy to evaluate the performance of a telescope, including its magnification, resolving power, field of view, exit pupil, surface brightness, and star magnitude limit, aiding in telescope design and observation planning.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Magnification: \[ M = \frac{f_o}{f_e}, \quad \text{where} \quad f_o = D_o \times f_r \] Resolving Power: \[ P_r = \frac{115.8}{D_o} \] True Field of View: \[ FOV_s = \frac{FOV_e}{M} \] Exit Pupil Diameter: \[ D_{ep} = \frac{D_o}{M} \] Surface Brightness: \[ SB = 2 \times D_{ep}^2 \] Star Magnitude Limit: \[ L_m = 2 + 5 \times \log_{10}(D_o) \] Where:

\( M \): Magnification (dimensionless)
\( f_o \): Focal length of the objective (mm)
\( f_e \): Focal length of the eyepiece (mm)
\( D_o \): Objective's diameter (mm)
\( f_r \): f-ratio (dimensionless)
\( P_r \): Resolving power (arcseconds)
\( FOV_e \): Apparent field of view of the eyepiece (degrees)
\( FOV_s \): True field of view (degrees)
\( D_{ep} \): Exit pupil diameter (mm)
\( SB \): Surface brightness (% of maximum light intensity per unit area)
\( L_m \): Star magnitude limit (magnitude)

Unit Conversions:

Length (\( D_o \), \( f_e \)): mm, cm (1 cm = 10 mm), in (1 in = 25.4 mm)

Steps:

Enter the objective's diameter (\( D_o \)), f-ratio (\( f_r \)), eyepiece focal length (\( f_e \)), and apparent field of view (\( FOV_e \)).
Convert \( D_o \) and \( f_e \) to mm if necessary.
Validate inputs: \( D_o \), \( f_r \), and \( f_e \) must be greater than 0; \( FOV_e \) must be between 30° and 110°.
Calculate the objective focal length: \( f_o = D_o \times f_r \).
Calculate the magnification: \( M = \frac{f_o}{f_e} \).
Calculate the resolving power: \( P_r = \frac{115.8}{D_o} \).
Calculate the true field of view: \( FOV_s = \frac{FOV_e}{M} \).
Calculate the exit pupil diameter: \( D_{ep} = \frac{D_o}{M} \).
Calculate the surface brightness: \( SB = 2 \times D_{ep}^2 \).
Calculate the star magnitude limit: \( L_m = 2 + 5 \times \log_{10}(D_o) \).
Display the results with 4 decimal places.

3. Importance of Telescope Magnification Calculation

Calculating telescope magnification and related parameters is crucial for:

Astronomical Observations: Determining the level of detail and the area of the sky visible through the telescope.
Telescope Design: Selecting the appropriate objective and eyepiece to achieve desired optical performance.
Image Quality Assessment: Evaluating resolving power, brightness, and visibility of faint objects.

4. Using the Calculator

Examples:

Example 1: For \( D_o = 100 \, \text{mm} \), \( f_r = 10 \), \( f_e = 25 \, \text{mm} \), \( FOV_e = 53 \, \text{degrees} \):
- Objective Focal Length: \( f_o = 100 \times 10 = 1000 \, \text{mm} \)
- Magnification: \( M = \frac{1000}{25} = 40 \)
- Resolving Power: \( P_r = \frac{115.8}{100} = 1.1580 \, \text{arcseconds} \)
- True Field of View: \( FOV_s = \frac{53}{40} = 1.3250 \, \text{degrees} \)
- Exit Pupil Diameter: \( D_{ep} = \frac{100}{40} = 2.5000 \, \text{mm} \)
- Surface Brightness: \( SB = 2 \times (2.5)^2 = 12.5000 \, \% \)
- Star Magnitude Limit: \( L_m = 2 + 5 \times \log_{10}(100) = 12.0000 \, \text{magnitude} \)
Example 2: For \( D_o = 8 \, \text{cm} \), \( f_r = 12 \), \( f_e = 1 \, \text{in} \), \( FOV_e = 53 \, \text{degrees} \):
- Convert: \( D_o = 8 \times 10 = 80 \, \text{mm} \), \( f_e = 1 \times 25.4 = 25.4 \, \text{mm} \)
- Objective Focal Length: \( f_o = 80 \times 12 = 960 \, \text{mm} \)
- Magnification: \( M = \frac{960}{25.4} \approx 37.7953 \)
- Resolving Power: \( P_r = \frac{115.8}{80} = 1.4475 \, \text{arcseconds} \)
- True Field of View: \( FOV_s = \frac{53}{37.7953} \approx 1.4023 \, \text{degrees} \)
- Exit Pupil Diameter: \( D_{ep} = \frac{80}{37.7953} \approx 2.1167 \, \text{mm} \)
- Surface Brightness: \( SB = 2 \times (2.1167)^2 \approx 8.9605 \, \% \)
- Star Magnitude Limit: \( L_m = 2 + 5 \times \log_{10}(80) \approx 11.5120 \, \text{magnitude} \)

5. Frequently Asked Questions (FAQ)

Q: What is telescope magnification?
A: Telescope magnification (\( M \)) is the ratio of the objective's focal length to the eyepiece's focal length, determining how much larger an object appears compared to the naked eye.

Q: Why is resolving power important?
A: Resolving power (\( P_r \)) indicates the smallest angular separation at which two objects can be distinguished, affecting the clarity of fine details in observations.

Q: What does the star magnitude limit tell us?
A: The star magnitude limit (\( L_m \)) indicates the faintest stars visible through the telescope; lower values mean brighter objects, and a lower \( L_m \) allows fainter objects to be seen.