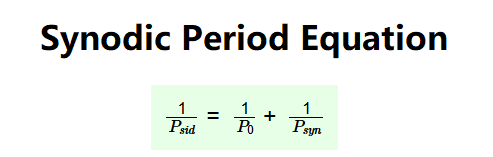Synodic Period Calculator

Input Mode:

Sidereal Period of Observed Planet (\( P_{sid} \)): yrs

Reference Planet's Sidereal Period (\( P_0 \)): yrs

1. What is Synodic Period Calculator?

Definition: This calculator computes the synodic period (\( P_{syn} \)) of a planet relative to a reference planet (typically Earth), based on the sidereal periods of both planets (\( P_{sid} \) and \( P_0 \)).

Purpose: It is used in astronomy to determine the time interval between successive alignments of a planet with the reference planet and the Sun, which is important for observing planetary motion and planning space missions.

2. How Does the Calculator Work?

The calculator uses the following equation for an inferior planet (closer to the Sun than the reference planet):

\( \frac{1}{P_{sid}} = \frac{1}{P_0} + \frac{1}{P_{syn}} \)

This can be rearranged to solve for the synodic period:

\( P_{syn} = \frac{P_{sid} \cdot P_0}{|P_0 - P_{sid}|} \)

Where:

\( P_{sid} \): Sidereal period of the observed planet (yrs)
\( P_0 \): Sidereal period of the reference planet (yrs, typically 1 year for Earth)
\( P_{syn} \): Synodic period (yrs)

Unit Conversions:

Synodic Period (\( P_{syn} \)):
- 1 year = 1 yr
- 1 year = 12 months
- 1 year = 365.25 days (approximate, accounting for leap years)

Steps:

Select the input mode (custom input or predefined planet).
If using custom input, enter the sidereal period of the observed planet (\( P_{sid} \)). If using a predefined planet, select the planet from the list and view its sidereal period.
Enter the sidereal period of the reference planet (\( P_0 \)), which defaults to 1 year (Earth's sidereal period).
Calculate \( P_{syn} \) using the equation above.
Convert the result to the selected unit for display (years, months, or days).
Display the result with 4 decimal places.

3. Importance of Synodic Period Calculation

Calculating the synodic period is crucial for:

Astronomical Observations: Determining the best times to observe a planet when it is aligned with the Sun and the reference planet (e.g., Earth).
Space Mission Planning: Scheduling launches to coincide with optimal planetary alignments for interplanetary travel.
Understanding Planetary Motion: Studying the relative motion of planets in the solar system.

4. Using the Calculator

Example: Calculate the synodic period of Mercury relative to Earth, given Mercury's sidereal period \( P_{sid} = 0.241 \, \text{yrs} \) and Earth's sidereal period \( P_0 = 1 \, \text{yr} \).

Select the input mode as "Predefined Planet" and choose "Mercury".
The calculator displays Mercury's sidereal period (\( 0.241 \, \text{yrs} \)).
Keep the reference planet's sidereal period as \( P_0 = 1 \, \text{yr} \) (default for Earth).
Click "Calculate" to compute:
- \( P_{syn} = \frac{P_{sid} \cdot P_0}{|P_0 - P_{sid}|} = \frac{0.241 \times 1}{|1 - 0.241|} = \frac{0.241}{0.759} \approx 0.3175 \, \text{yrs} \)
- In days: \( 0.3175 \times 365.25 \approx 115.9669 \, \text{days} \), which is close to the known synodic period of Mercury (about 116 days).

5. Frequently Asked Questions (FAQ)

Q: What is the synodic period?
A: The synodic period (\( P_{syn} \)) is the time interval between successive alignments of a planet with the reference planet (e.g., Earth) and the Sun, as observed from the reference planet.

Q: What is the sidereal period?
A: The sidereal period (\( P_{sid} \)) is the time it takes for a planet to complete one full orbit around the Sun relative to the fixed stars.

Q: Why does the reference planet's sidereal period default to 1 year?
A: The reference planet is typically Earth, which has a sidereal period of approximately 1 year (365.25 days). This default value simplifies calculations for observing other planets from Earth.