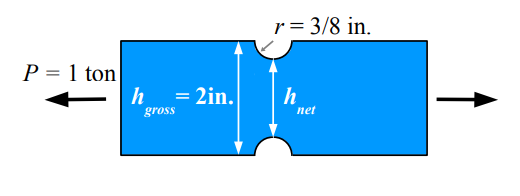
Stress Concentration Calculator With Groove
Unit Converter ▲
Unit Converter ▼
1. What is the Stress Concentration Calculator?
Definition: The Stress Concentration Calculator determines the maximum stress in a bar with semicircular grooves using the formula \(\sigma_{max} = K \cdot \frac{P}{A_{net}}\), reporting the result in ksi.
Purpose: Assists engineers in analyzing stress concentration due to geometric discontinuities.
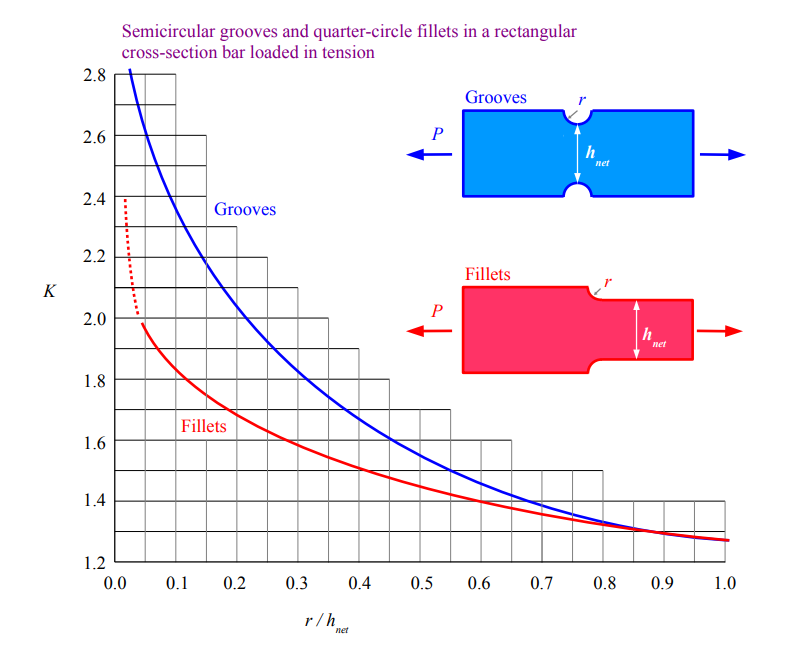
Reference:Applied Strength of Materials for Engineering Technology
http://www.etcs.pfw.edu/~dupenb/ET_200/Applied%20Str%20of%20Mat%20for%20ET%20v14%20July%202018.pdf
2. How Does the Calculator Work?
Formula:
\(\sigma_{max} = K \cdot \frac{P}{A_{net}}\)
Where:
- \(\sigma_{max}\): Maximum stress (ksi)
- \(K\): Stress concentration factor
- \(P\): Load (kip)
- \(A_{net}\): Net cross-sectional area (in²)
Steps:
- Step 1: Input Load. Enter the load value (e.g., 1 ton, 2 kip).
- Step 2: Input Gross Width. Enter the gross width (e.g., 2 in).
- Step 3: Input Radius. Enter the radius of the groove (e.g., 0.375 in).
- Step 4: Input Thickness. Enter the thickness (e.g., 0.25 in).
- Step 5: Calculate. The calculator computes the maximum stress in ksi.
3. Importance of Stress Concentration Calculation
Calculating stress concentration is crucial for:
- Material Strength: Identifies potential failure points.
- Design Safety: Ensures structures withstand concentrated loads.
4. Using the Calculator
Example:
Load = 1 ton, Gross Width = 2 in, Radius = 3/8 in, Thickness = 0.25 in:
- Step 1: \( P = 2 \, \text{kip} \).
- Step 2: \( h_{net} = 2 - 2 \cdot 0.375 = 1.25 \, \text{in} \).
- Step 3: \( A_{net} = 1.25 \cdot 0.25 = 0.3125 \, \text{in}^2 \).
- Step 4: \( K \approx 1.82 \).
- Step 5: \(\sigma_{max} \approx 11.6 \, \text{ksi}\).
5. Frequently Asked Questions (FAQ)
Q: What is stress concentration?
A: Stress concentration is the increase in stress near geometric discontinuities.
Q: Why use ksi?
A: Ksi is a common unit for stress in engineering calculations.
Stress Concentration Calculator© - All Rights Reserved
 Home
Home
 Back
Back