1. What is Stokes' Law Calculator?
Definition: This calculator computes the terminal velocity (\( v \)) of a spherical particle in a viscous fluid, based on the particle diameter (\( d \)), particle density (\( \rho_p \)), fluid density (\( \rho_m \)), and dynamic viscosity of the fluid (\( \mu \)).
Purpose: It is used in physics and engineering to determine the settling velocity of particles in fluids, applicable in sedimentation processes, atmospheric science (e.g., raindrop settling), and biological studies (e.g., cell sedimentation).
2. How Does the Calculator Work?
The calculator uses the following formula:
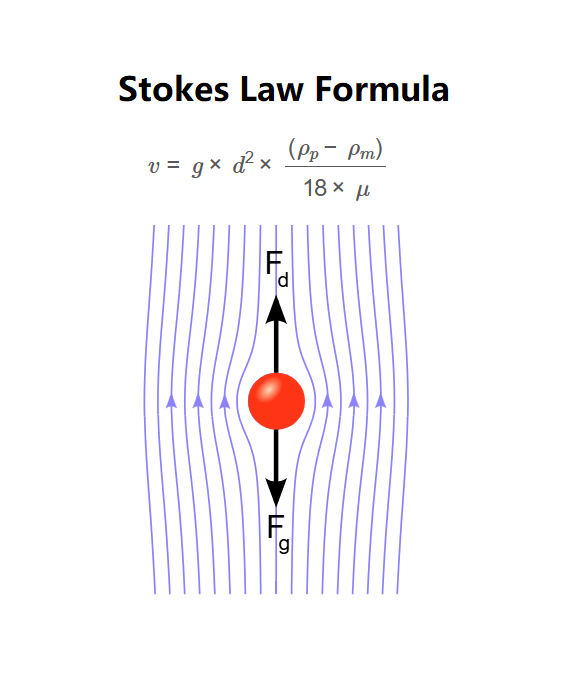
Formula:
\[
v = g \times d^2 \times \frac{(\rho_p - \rho_m)}{18 \times \mu}
\]
Where:
- \( v \): Terminal velocity (m/s, ft/s, km/h, mph)
- \( g \): Gravitational acceleration on Earth, 9.80665 m/s²
- \( d \): Particle diameter (m, cm, mm, in)
- \( \rho_p \): Particle density (kg/m³, lb/ft³)
- \( \rho_m \): Fluid density (kg/m³, lb/ft³)
- \( \mu \): Dynamic viscosity (Pa·s, cP)
Unit Conversions:
- Particle Diameter (\( d \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 in = 0.0254 m
- Density (\( \rho_p \), \( \rho_m \)):
- 1 kg/m³ = 1 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³
- Dynamic Viscosity (\( \mu \)):
- 1 Pa·s = 1 Pa·s
- 1 cP = 0.001 Pa·s
- Terminal Velocity (\( v \)):
- 1 m/s = 1 m/s
- 1 ft/s = 1 / 0.3048 m/s
- 1 km/h = 1 / 3.6 m/s
- 1 mph = 1 / 0.44704 m/s
Steps:
- Enter the particle diameter (\( d \)) with its respective unit (m, cm, mm, in).
- Enter the particle density (\( \rho_p \)) with its respective unit (kg/m³, lb/ft³).
- Enter the fluid density (\( \rho_m \)) with its respective unit (kg/m³, lb/ft³).
- Enter the dynamic viscosity (\( \mu \)) with its respective unit (Pa·s, cP).
- Convert all inputs to SI units (m for \( d \), kg/m³ for \( \rho_p \) and \( \rho_m \), Pa·s for \( \mu \)).
- Calculate the terminal velocity (\( v \)) using the formula with \( g = 9.80665 \, \text{m/s²} \).
- Convert the result to the selected unit and display it, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Stokes' Law Calculation
Calculating terminal velocity using Stokes' Law is crucial for:
- Sedimentation Processes: Determining the settling rate of particles in liquids, such as in water treatment or geological sedimentation.
- Atmospheric Science: Estimating the fall speed of raindrops or dust particles in the atmosphere.
- Biological Applications: Analyzing the sedimentation of cells or particles in biological fluids, such as in centrifugation processes.
4. Using the Calculator
Examples:
- Example 1: Calculate the terminal velocity of a spherical particle with a diameter of 0.1 mm, particle density of 2500 kg/m³, in a fluid with density 1000 kg/m³ and dynamic viscosity 0.001 Pa·s, with the result in m/s:
- Enter \( d = 0.1 \) mm.
- Convert to m: \( d = 0.1 \times 0.001 = 0.0001 \, \text{m} \)
- Enter \( \rho_p = 2500 \) kg/m³.
- Enter \( \rho_m = 1000 \) kg/m³.
- Enter \( \mu = 0.001 \) Pa·s.
- Terminal velocity: \( v = 9.80665 \times (0.0001)^2 \times \frac{(2500 - 1000)}{18 \times 0.001} = 9.80665 \times 0.00001 \times \frac{1500}{0.018} = 8.1722 \times 10^{-3} \, \text{m/s} \)
- Result: \( v = 8.1722 \times 10^{-3} \, \text{m/s} \)
- Example 2: Calculate the terminal velocity of a spherical particle with a diameter of 0.02 in, particle density of 150 lb/ft³, in a fluid with density 62.4 lb/ft³ and dynamic viscosity 1 cP, with the result in ft/s:
- Enter \( d = 0.02 \) in.
- Convert to m: \( d = 0.02 \times 0.0254 = 0.000508 \, \text{m} \)
- Enter \( \rho_p = 150 \) lb/ft³.
- Convert to kg/m³: \( \rho_p = 150 \times 16.0185 = 2402.775 \, \text{kg/m³} \)
- Enter \( \rho_m = 62.4 \) lb/ft³.
- Convert to kg/m³: \( \rho_m = 62.4 \times 16.0185 = 999.5544 \, \text{kg/m³} \)
- Enter \( \mu = 1 \) cP.
- Convert to Pa·s: \( \mu = 1 \times 0.001 = 0.001 \, \text{Pa·s} \)
- Terminal velocity: \( v = 9.80665 \times (0.000508)^2 \times \frac{(2402.775 - 999.5544)}{18 \times 0.001} = 9.80665 \times 0.000000258064 \times \frac{1403.2206}{0.018} = 0.1973 \, \text{m/s} \)
- Convert to ft/s: \( v = 0.1973 \times 3.28084 = 0.6473 \, \text{ft/s} \)
- Result: \( v = 0.6473 \, \text{ft/s} \)
5. Frequently Asked Questions (FAQ)
Q: What does Stokes' Law describe?
A: Stokes' Law describes the terminal velocity of a spherical particle falling through a viscous fluid under the influence of gravity, assuming laminar flow conditions.
Q: What are the limitations of Stokes' Law?
A: Stokes' Law applies only to small spherical particles in laminar flow (low Reynolds number), and it assumes no turbulence, no particle interaction, and a Newtonian fluid.
Q: Why is gravitational acceleration fixed at 9.80665 m/s²?
A: The value 9.80665 m/s² is the standard gravitational acceleration on Earth, used for consistency in calculations unless specified otherwise (e.g., on another planet).
 Home
Home
 Back
Back